EN中文

地理科学进展 >

2014 , Vol. 33 >Issue 8: 1058 - 1067

DOI: https://doi.org/10.11820/dlkxjz.2014.08.006

信阳城市人口—城区用地异速生长分析

  • 陈彦光 , 1 ,
  • 张莉 2
展开
  • 1. 北京大学 城市与环境学院城市与经济地理系,北京 100871
  • 2. 中国城市规划设计研究院城乡规划研究室,北京 100044

作者简介:陈彦光(1965-),男,河南罗山人,博士,教授,主要从事城市地理学、理论地理学以及计量地理学研究,E-mail:。

网络出版日期: 2014-08-25

基金资助

国家自然科学基金项目(41171129)

收起

An allometric analysis of the scaling relations between population and urban area of Xinyang

  • CHEN Yanguang , 1 ,
  • ZHANG Li 2
Expand
  • 1. Department of Geography, College of Urban and Environmental Sciences, Peking University, Beijing 100871, China
  • 2. Department of Urban and Rural planning, China Academy of Urban Planning and Design, Beijing 100044, China

Online published: 2014-08-25

Copyright

《地理科学进展》杂志 版权所有
Fold

摘要

城市人口规模和用地面积随着时间的改变过程理论上服从异速生长定律,即在一定时空范围内表现为幂指数关系,并且标度指数小于1。但由于种种原因,中国的统计数据大多不满足纵向异速标度关系,或者标度指数严重异常。为深入研究这一问题,借助最小二乘法和对数线性回归分析技术,基于信阳的人口普查数据和城市用地现状图资料,开展城市人口和城市用地面积的标度分析,发现城市生长长期服从纵向异速生长定律,可用幂函数描绘,并且标度指数(约为0.86)接近于理论预期值(0.85)。然而,由于近年的“造城运动”,这种标度关系遭到破坏,城市人—地关系出现混乱。因此,揭示城市演化规律的前提是数据质量的保证,而人文系统的规律也会因为人为的因素而暂时破坏。本文提供了一个城市纵向异速生长及其标度破坏的简明案例,并给出了估计和预测信阳城市人口和用地的数学模型,其计算结果可以作为了解同类城市人—地关系的演化进程和未来趋势的重要参考。

关键词： 异速生长; 异速标度; 分维; 标度间断; 城市人—地关系; 信阳

本文引用格式

陈彦光 , 张莉 . 信阳城市人口—城区用地异速生长分析[J]. 地理科学进展, 2014 , 33(8) : 1058 -1067 . DOI: 10.11820/dlkxjz.2014.08.006

Abstract

The relationship between urban population and construction land area is supposed to follow the law of allometric growth, which is based on exponential growth or distribution. However, if we apply the allometric scaling law to Chinese cities using data from the statistical yearbooks of China, the relationship is often unclear or unconvincing, possibly due to the quality of the statistical data used. In this study, the ordinary least square method and log-linear regression analysis are employed to make a longitudinal allometric analysis of urban evolution of Xinyang, a medium-sized city of Henan Province, China. Population of the urban area (which is greater than the non-agricultural population of the same city) was estimated by using the census data from multiple years; the area of urban construction land was estimated using the land-use maps. The quality of these data is clearly higher than those provided in the statistical yearbooks. The result of the analysis shows that from 1949 to 2004, the urban population and area of construction land in Xinyang followed the allometric scaling law. During the period between 2007 and 2013, the scaling relation was disrupted due to the "city-making movement" in the context of an overheated economy based on real estate development and rapid urbanization. The following conclusion can be drawn: the urban evolution of Chinese cities follows the allometric growth law, but the allometric scaling can be disturbed by government policies in a largely command and control economy. The significance of this work lies in that, first, it provides a typical case of longitudinal allometry of China's cities for urban studies; second, it gives a set of models that can be used to estimate and project population size and urban land area of cities like Xinyang; and third, it lays a foundation for future allometric studies based on logistic growth rather than exponential growth.

Key words： allometric growth; allometric scaling; fractal dimension; scaling breaking; urban human-environment relation; Xinyang

1 引言

城市的演化过程及其空间格局遵循一定的规律性,其中的重要法则之一就是异速生长定律(Carroll, 1982; Lee, 1989; Batty et al, 1994; 周一星, 1999; Lo, 2002)。异速生长(allometric growth),顾名思义,就是指城市系统的各个部分发育的相对速度不同。所谓异速生长定律是指城市系统的一个要素(如人口)的相对增长率与另外一个要素(如土地)的相对增长率构成固定的比例关系(陈彦光, 2013)。异速分析在城市地理学理论和实践中有着广泛的应用,讨论最多的是城市人口—城区用地之间的异速生长或者几何测度关系(Lo et al, 1977; 陈彦光等, 1999, 2001, 2004; 刘继生等, 2000, 2004, 2005; 陈彦光, 2002; 梁进社等, 2002; 李郇等, 2009; 赵岑等, 2010)。城市人口规模和城区用地面积之间的标度关系代表了一种城市人地关系,该关系背后隐含着城市演化的空间动力学。然而,如果借助中国各地统计年鉴提供的城市人口和城区面积时间序列(样本路径)拟合城市人口—城区面积异速关系,会发现统计分析结果通常不能令人满意:要么点、线匹配效果不好,要么模型参数超出正常范围。出现这种情况的原因可能有两个:一是中国城市不遵循异速生长定律;二是中国的统计数据质量没有达标。中国的城市概念不同于西方的城市概念,西方城市如美国城市有比较严格和规范的统计学标准(Rubenstein, 1999; 陈彦光, 2008)。然而,中国的城市没有这样一套完整和公认的法定标准,城市人口和用地统计范围比较随意,地方政府也常常根据各自的需要主观地改变城市的定义。加之统计数据获取过程中存在的种种问题,造成中国城市统计资料质量普遍公信力不强。利用这种数据探索城市演化规律,无法取得可信的结果。
最近,作者在信阳城市调查、研究过程中,取得了一组不同年份城市人口规模和建设用地面积的数据。这套数据样本点虽不多,但较之于统计年鉴提供的数据,质量相对可靠,且时间跨度较长,可望比较有效地反映城市人—地关系的演化特征和规律。信阳是河南省南部的一个地级市,地理位置独特,属南北与东西的过渡地带,虽然目前规模不大,但前景很好,值得研究。该数据表明,信阳的城市发展长期遵循异速生长定律,并且标度指数与理论预期非常接近。这个标度关系直到近年才被房地产业激发的“造城运动”打破。本文利用上述数据研究信阳城市人口和建设用地面积的异速生长关系及其标度断裂的前因后果。研究价值体现在以下几个方面:①为理论研究提供一个中国城市人口—城区面积异速关系的案例。这个案例对发展中国城市异速生长理论具有参考作用。②为研究与信阳同类的规模不大但前景较好的地级中等城市提供一套人口规模和用地面积估计与预测的数学模型。利用这些模型,可以基于条件平均的思想重构人口和用地的历史数据,并且对未来增长趋势进行适当的预测。③尤为重要的是,为发展异速生长理论打开了一扇新的窗口。传统的异速生长模型是基于指数增长过程的,而本文提供了基于Logistic增长过程探索异速标度分析方法的新思路。

2 模型与数据

2.1 数学模型

异速生长可以分为纵向异速(longitudinal allometry)和横向异速(cross-sectional allometry)两大基本类别。纵向异速描述的是时间演化中的动态过程,其观测资料为时间序列或其样本路径;横向异速描述的是空间分布中的静态格局,其观测资料为等级序列或者截面数据(Naroll et al, 1956; Lee, 1989; 陈彦光, 2010)。对于单个城市的演化过程,只能采用纵向异速生长模型开展分析,其数学表达为:
式中:t表示时序或年份;At为时刻t的城市面积;Pt为相应时刻的城市人口规模;参数a为比例系数,b为标度指数。对式(1)求时间t的导数可得:
可见,所谓城市人口—城区面积的异速生长定律是指城市面积的相对增长率与城市人口的相对增长率的比值为常数,这个常数就是异速标度指数b。
理论上,一个异速生长关系可以从两个指数生长过程推导过来(Bertalanffy, 1968)。换言之,式(1)的背后存在两个指数增长,一个是城市人口的指数增长,另一个是城市面积的指数增长,表达式如下:
式中:P0为城市人口初始值(第一个时刻的数值);A0为城市面积初始值;rp=dPt/(Pt dt)为城市人口的相对增长率;ra=dAt/(Atdt)为城区面积的相对增长率。因此理论上必有b=ra/rp 。
指数增长是一种无约束的增长。如果一个增长过程受到自然条件的限制或者约束,则增长过程为Logistic增长(Bertalanffy, 1968)。Logistic增长曲线为S形,前半段近似为指数增长,后半段类似于对数增长。城市人口和城市面积的Logistic增长模型为:
式中:Pmax为城市人口最大值(容量或者承载量参数);Amax为城市面积最大值;kp为城市人口的初始增长率;ka为城区面积的初始增长率。显然,容量参数数值较大,当时序t不是很大时,Logistic增长模型可以近似为指数增长模型。因此,当人口规模Pt<Pmax/2、用地面积At<Amax/2时,式(1)反映的异速生长关系依然成立(Chen, 2014a)。

2.2 测度与数据资料

采用两个基本测度描述城市人口—城区面积的异速生长关系。人口规模采用城区人口,其口径要比住建部提供的非农业人口规模大。城区面积则采用城市建设用地面积的总和,这个数值与建成区面积非常接近。数据资料来源于中国城市规划设计研究院信阳城市总体规划课题组。人口数据是根据历次人口普查数据,按照一定的统计学标准推算;城市用地面积则是根据不同年份的城市用地现状图,利用计算机图像处理技术提取的数据。全部人口和面积数据的提取与计算工作由中国城市规划设计研究院专家完成。由于信阳城市用地现状图不多,只有6个年份的资料,人口数据的推测也仅仅给出了6个年份的结果,与用地年份对应(表1)。相对于统计年鉴提供的有关数据,这套数据更为客观、可靠。尤其可贵的是,这套数据的人口计算范围与用地计算范围大体一致。
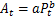
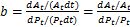
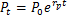
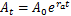
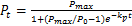
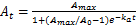
Tab.1 Urban population and area of urban construction land in Xinyang

表1 信阳城市人口和城市建设用地面积观测值

年份(n) 1949 1979 1993 1999 2004 2013
时序(t=n-1949) 0 30 44 50 55 64
人口(Pt)/万人 3.7 15.0 33.0 32.0 46.0 67.0
面积(At)/km2 4.50 17.15 25.10 31.63 42.89 89.11

3 结果与分析

考察表1的数据发现,1949-2004年,信阳城市人口和城市建设用地总面积之间很好地满足纵向异速生长关系。在城市人口—城区面积坐标图中可以清楚地看出,1949-2004年这个时间段的数据点服从式(1)所示的幂指数关系,而2013年的数据点则偏离了这个趋势线,表现为一个异常值(图1)。相对于2013年的用地面积而言,城市人口规模太小;相对于城市人口规模来说,城市建设面积太大。将表1中1949-2004年间的5个观测值(由于标度间断,2013年的观测值即图中圆点作为异常点处理,不参与标度指数计算)拟合式(1)所示的异速生长关系,借助最小二乘法,得到如下模型(图1):
式中:Pt为城市人口;At为城市建设用地面积,尖冒号“ˆ”表明是估计值(下同);拟合优度R2=0.9817。标度指数b=0.8605(标准误差为0.0678),非常接近于理论预期值0.85(陈彦光等, 1999; Chen, 2010)。这个模型的剩余自由度为3,拟合结果通过0.01的显著性水平检验。如果将2013年的数据点计算在内(6个观测值,自由度为4),利用表1中的全部数据拟合式(1),大体也服从异速生长关系,但拟合效果较式(7)相差较大,模型为:
拟合优度R2=0.9618,标度指数约为0.9498(标准误差为0.0947),置信度依然在99%以上。2004-2013年,异速标度指数约为1.4856,高出理论预期范围。但由于自由度太低,这个数值的置信度无法判断,仅供参考。
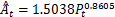
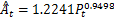
Fig.1 Allometric relationship between urban population and area of urban construction land in Xinyang, 1949-2004/2013

图1 信阳城市人口—城区面积异速生长关系(1949-2004/2013)

进一步研究发现,信阳城市人口和城市建设用地面积都表现出指数增长趋势。1949-2013年间,信阳城市人口可以很好地拟合指数增长模型,拟合优度为0.9911(图2a);1949-2004年间,信阳城市建设用地面积可以更好地拟合指数增长模型,拟合优度为0.9923(图2b)。对于城市用地的指数增长而言,2013年的数据表现为异常值。如果将2013年的数值包括在内,也可以拟合指数增长,但效果差一些,拟合优度约为0.9738。这些模型的置信度都在99%以上。
Fig.2 Exponential growth of urban population and area of urban construction land in Xinyang, 1949-2004/2013

图2 信阳城市人口和城市用地面积指数增长图式(1949-2013)(由于标度间断,2013年的城市用地观测值即图中圆点作为异常值处理,不参与模型拟合)

指数增长代表一种无局限的增长,理论上它会永远增长下去。然而,在现实中,这个过程是不可能出现的。任何事物的增长都受到时空条件的限制,指数增长模型仅仅在一定时空尺度范围内成立。由于地理空间、自然资源、基础设施、吸引能力、生态环境对城市废物的降解能力等方面限制,城市人口和城市建设用地的增长势必有一个上限。从长期看来,信阳城市人口和城市用地面积增长都服从Logistic模型。Logistic函数属于三参数模型,其参数估计要比异速生长关系之类的二参数模型复杂得多。有以下3种方法用于估计Logistic模型参数:①非线性拟合,需借助Matlab之类的软件实现(陈彦光, 2012b);②自回归方法,可以通过Excel或者Matlab完成,但对数据的连续性和样本路径长度有要求(陈彦光, 2009a, 2010, 2012a);③容量(承载量)参数的蛮力搜索法,这个方法虽然笨拙,但参数估计效果很好,借助Excel即可达到目的(陈彦光, 2010)。采用蛮力搜索法,根据1949-2013年的数据,得到信阳城市人口的Logistic增长模型:
拟合优度R2=0.9914。这个模型既可用于对1949-2013年间的人口规模进行插值和重构,也可以用于对2013年之后的人口增长进行预测分析(图3)。根据1949-2004年的数据,基于蛮力搜索法,得到信阳城市建设用地的Logistic增长模型:
拟合优度R2=0.9925,这里没有考虑2013年异常点。这个模型可用于对1949-2004年间的用地规模进行插值和重构,但不能用于对2013年之后的用地增长进行有效预测(图4)。
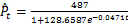
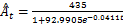
Fig.3 Logistic growth curve of urban population in Xinyang, 1949-2030

图3 信阳城区非农业人口的Logistic增长曲线(1949-2030)

Fig.4 Logistic growth curves of area of urban construction land in Xinyang, 1949-2030

图4 信阳城市建设用地面积的增长曲线(1949-2030)

如果将2013年的数值考虑在内,则无法有效拟合Logistic曲线,但可近似拟合指数增长曲线,因为最大值不能收敛到一个稳定的容量参数。不过指数预测意味着城市用地面积无休止增长下去,这类模型对于远期增长预测没有意义。在这种情况下,可以考虑拟合二次方Logistic生长方程:
从长远看,城市用地总量是一定的,故不必搜索Amax值,直接根据式(10)取Âmax=435即可。将表1中的城市用地数据拟合上式,得到如下模型:
拟合优度R2=0.9486。这个模型的优点是能够对2013年前后10年左右的数值进行重建和预测,但对早期的数值不能准确重构,对未来远期的增长也不能有效预测(图4)。
借助上述模型,对信阳市历年的城市人口规模和用地面积进行估计(1949-2004年)和预测(2013-2030年)。人口预测只有一种方法,那就是利用式(9)直接估计1949-2013年的城市人口,并预测2014-2030年的人口规模。城市建设用地预测则至少有4种预测途径:前两种途径是利用式(10)和式(12)直接估计和预测,后两种途径是借助式(7)和式(8),在式(9)给出的人口计算结果基础上间接估计和预测(表2)。可以看出,城市用地的Logistic模型预测结果和第一种异速生长模型间接估计的结果没有显著性的差别,因为这两种模型都是基于1949-2004年的数据构建的,没有考虑2013年的异常值。二次Logistic模型预测和第二种异速生长模型的间接估计结果与前两种结果存在显著差异,因为后两种预测受到2013年数值的影响。下文将结合信阳城市演化对这些预测结果进行评价。
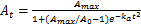
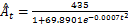
Tab.2 Estimated(1949-2004) and projected(2013-2030) non-agricultural population and area of urban construction land in Xinyang

表2 信阳城市人口和城市建设用地面积估计值和预测值

年份
n		 时序
t		 人口规模Pt /万人 建设用地面积At /km2
Logistic预测值 Logistic预测 二次logistic预测 异速生长预测1 异速生长预测2
1949 0 3.76 4.63 6.14 4.70 4.30
1950 1 3.94 4.82 6.14 4.89 4.50
1951 2 4.12 5.02 6.15 5.09 4.70
1952 3 4.32 5.23 6.17 5.30 4.91
1953 4 4.53 5.44 6.21 5.52 5.14
1954 5 4.74 5.67 6.24 5.74 5.37
1955 6 4.97 5.90 6.29 5.98 5.61
1956 7 5.21 6.15 6.35 6.22 5.87
1957 8 5.46 6.40 6.42 6.48 6.13
1958 9 5.72 6.67 6.49 6.74 6.41
1959 10 5.99 6.94 6.58 7.02 6.70
1960 11 6.27 7.23 6.68 7.30 7.00
1961 12 6.57 7.53 6.78 7.60 7.32
1962 13 6.89 7.84 6.90 7.91 7.65
1963 14 7.21 8.16 7.03 8.23 8.00
1964 15 7.56 8.50 7.18 8.57 8.36
1965 16 7.91 8.85 7.34 8.92 8.73
1966 17 8.29 9.21 7.51 9.28 9.12
1967 18 8.68 9.59 7.69 9.66 9.53
1968 19 9.09 9.98 7.89 10.05 9.96
1969 20 9.52 10.39 8.11 10.46 10.41
1970 21 9.97 10.81 8.34 10.88 10.88
1971 22 10.44 11.26 8.59 11.32 11.36
1972 23 10.94 11.71 8.87 11.78 11.87
1973 24 11.45 12.19 9.16 12.26 12.40
1974 25 11.99 12.69 9.48 12.75 12.96
1975 26 12.55 13.21 9.82 13.26 13.53
1976 27 13.14 13.74 10.18 13.80 14.14
1977 28 13.76 14.30 10.58 14.35 14.77
1978 29 14.40 14.88 11.00 14.93 15.42
1979 30 15.08 15.48 11.46 15.53 16.11
1980 31 15.78 16.11 11.95 16.15 16.82
1981 32 16.52 16.76 12.48 16.80 17.56
1982 33 17.29 17.43 13.05 17.47 18.34
1983 34 18.09 18.13 13.67 18.16 19.15
1984 35 18.93 18.86 14.33 18.89 19.99
1985 36 19.80 19.61 15.04 19.63 20.87
1986 37 20.72 20.40 15.81 20.41 21.78
1987 38 21.67 21.21 16.64 21.22 22.73
1988 39 22.67 22.06 17.53 22.06 23.73
1989 40 23.71 22.93 18.50 22.93 24.76
1990 41 24.80 23.84 19.54 23.83 25.83
1991 42 25.93 24.79 20.67 24.76 26.95
1992 43 27.11 25.77 21.89 25.73 28.12
1993 44 28.34 26.78 23.20 26.73 29.33
1994 45 29.63 27.83 24.63 27.77 30.59
1995 46 30.96 28.92 26.17 28.85 31.90
1996 47 32.36 30.05 27.83 29.96 33.27
1997 48 33.81 31.22 29.64 31.11 34.68
1998 49 35.32 32.43 31.59 32.31 36.16
1999 50 36.90 33.69 33.71 33.54 37.69
2000 51 38.54 34.99 36.00 34.82 39.27
2001 52 40.24 36.34 38.48 36.14 40.92
2002 53 42.02 37.73 41.17 37.51 42.63
2003 54 43.86 39.17 44.08 38.92 44.41
2004 55 45.78 40.66 47.24 40.38 46.25
2005 56 47.77 42.20 50.65 41.89 48.16
2006 57 49.84 43.79 54.34 43.45 50.14
2007 58 51.99 45.44 58.33 45.05 52.19
2008 59 54.22 47.14 62.64 46.71 54.31
2009 60 56.53 48.89 67.30 48.42 56.51
2010 61 58.93 50.70 72.32 50.18 58.79
2011 62 61.41 52.57 77.72 52.00 61.14
2012 63 63.99 54.50 83.53 53.87 63.57
2013 64 66.65 56.49 89.77 55.79 66.08
2014 65 69.41 58.54 96.45 57.77 68.67
2015 66 72.26 60.66 103.59 59.81 71.35
2016 67 75.21 62.83 111.21 61.90 74.11
2017 68 78.25 65.08 119.30 64.05 76.96
2018 69 81.40 67.38 127.88 66.26 79.89
2019 70 84.64 69.76 136.94 68.53 82.92
2020 71 87.99 72.20 146.48 70.85 86.03
2021 72 91.44 74.71 156.47 73.24 89.22
2022 73 94.99 77.28 166.90 75.68 92.51
2023 74 98.64 79.93 177.72 78.18 95.89
2024 75 102.40 82.65 188.91 80.73 99.36
2025 76 106.26 85.43 200.41 83.35 102.91
2026 77 110.23 88.29 212.15 86.02 106.56
2027 78 114.30 91.22 224.08 88.74 110.29
2028 79 118.47 94.22 236.13 91.52 114.11
2029 80 122.75 97.29 248.21 94.36 118.02
2030 81 127.12 100.43 260.25 97.25 122.01

4 讨论

前面的计算结果表明,信阳城市演化具有明显的规律性:①从1949-2004年,城市人口规模和建设用地关系长期保存异速生长关系;②这期间异速标度指数b≈0.8605,接近于理论预期值0.85(图1)。经验上,城市人口—城区面积异速标度指数的合理范围为2/3~1,即2/3<b<1。异速标度指数的本质是城市形态的分维D与城市人口的维数d=2之间的比值。城市形态的理想分维约为D=1.7,故异速标度指数的理想数值约为b=D/d≈0.85(Chen, 2010)。从这个意义上讲,1949-2004年间,信阳城市人口与建设用地关系是合理的。随着人口规模的增长,城市向高层发展,人均用地逐步减少,城市用地节约。根据式(7),人均用地随城市规模的增长呈负幂律衰减:
可见,城市人口每增加一个单位,城市用地增加一般不到一个单位。城市人口每增加一个相对的份额,城市用地增加大约0.86个相对的份额,这个过程原本要一直持续到2050年前后。
然而,到了2013年,上述标度关系受到了破坏,城市用地显著高于理论预期。根据城区人口规模和正常的异速标度关系,2013年的城市用地面积的合理数值是56 km2左右。然而,实际上这一年的城市用地面积达到89.11 km2,超支大约33 km2。因此,2013年的城市人地关系数据点明显偏离趋势线,表现为异速生长的标度间断。所谓标度间断(scaling break),就是从某个尺度或者时刻开始,标度指数发生了突变或者跳跃。如前所述,2004年之前,信阳异速标度指数约为0.86;2004年之后,则突然上升到1.49左右,表明信阳城市人地关系出现明显失调。从城市建设发展过程来看,2003年2月,信阳市领导班子换届后,当地政府着手筹建羊山新区。新区起步面积为30.7 km2,规划总面积达76 km2,而2004年全市实际用地总面积也只有42.89 km2。2006年11月,领导班子再次换届,原来的市长出任市委书记,随后羊山新区开始大规模建设。于是,一座表面光鲜、整洁的新城拔地而起。但由于赶速度、抢时间,地下排水管道等看不见的市政设施敷衍了事。这都为城市的长远健康发展留下了隐患。综上所述,异速标度指数的异常上升以及城市建设的实际情况,说明如今快速城市化背景下的“造城运动”对城市演化具有显著的破坏力。
城市化有其自身的内在规律和一些隐含的不变特性。人为的造城运动只能导致土地城市化和助长房地产泡沫,但不能推动真正的城市化。城市化不仅包括人口迁移到城市和城市形态的改变,还涉及人口的非农化、生活习惯和观念的城市化(urbanism),以及大尺度上的城市体系的演化(Knox et al, 2009)。羊山新区是典型的自上而下型城市化的结果,没有与自下而上的城市自发演化过程(自组织)很好地对接。信阳羊山新区建设之后,出现以下一些问题:①新区功能不全。虽然在行政命令的干预下,一些城市职能部门迁移到新区,但学校、医院、大型购物中心、菜市场等等城市基本成分没有成长起来,市民生活不便。②房价太高。普通居民购买不起这里的房子,买房的大多是信阳的炒房者和外地人(留待退休之后居住)。③城市就业容量不足。城市化是以工业化为前提的,缺乏产业支撑,乡村人口无法向城市迁移,即便购买了信阳的房子,也无法实现及时的非农化。况且,随着信息化时代的到来,网络改变了人们的聚集方式。在这种情况下,城市用地面积骤然扩张,但城市人口依然按照过去的相对速度增长。于是,城市人—地标度关系遭到破坏。
Logistic增长暗示城区人口和建设用地面积增长先加速后减速。借助容量参数即人口和建设用地的最大值,可以判断速度的顶峰。当城区人口达到最大值的一半,即Pmax/2=243.5时,人口速度最大;当城市面积达到最大值的一半,即Amax/2=217.5时,建设用地增长速度最大。如果信阳的城市人—地异速标度关系没有被扰乱,则大约在2052-2053年前后,人口增长速度达到极限,此前加速,此后减速;2059-2060年前后,城市建设用地速度达到极限,此前加速,此后减速(图5,假定标度没有破坏,根据式(9)和式(10)绘制)。原则上,城区人口与城市用地面积的增长应该同步,但实际上城市人口的增长先于城区用地的增长,二者之间存在一个时间滞后(Chen, 2014a)。信阳的滞后期大约7~8年。正因为如此,城市人口Zipf分布的标度区(scaling range)范围大于城区面积Zipf分布的标度区范围。由于羊山新区的造城运动,信阳城市形态突然快速扩展,原本滞后的城市用地超越城市人口后来居上。
Fig.5 Unimodal curves of growth rates of urban population and area of urban construction land in Xinyang, 1949-2200

图5 信阳城区人口和建设用地面积的增长速度(1949-2200)

城市人—地关系的破坏导致以下后果:①城市用地浪费惊人。不独信阳如此,这个问题在全国都非常普遍。昆明、郑州、常州、营口、鄂尔多斯等二、三线城市,都出现了新区成为“鬼区”,新城变成“鬼城”的现象,造成了土地资源和资金的巨大浪费。②城市用地的增长难以预测,给城市规划带来不便。在表2中,城市用地的Logistic预测和第一种异速生长预测都是基于1949-2004年的数据信息建模完成的,可以用于对过去的用地数量进行估计和重构,但不能预测今后的城市用地面积。二次Logistic模型可以用于最近5年的城市用地预测,但越是远期,预测越不可靠。信阳市今后的城市用地合理范围应该采用第二种异速生长方程预测。近期可能高于这套数值,但远期要逐步向这套数值回归。这第二种模型给出的城市用地承载量是约为437,与式(10)预计的承载量参数值435非常接近。
本文不足之处是样本太少,只有6个观测点,参数的误差范围较大。尽管如此,统计分析都是作置信陈述(confidence statement),而不是提供绝对结论。一个完整的置信陈述包括两个组成部分:一是判断的置信水平(level of confidence),二是参数估计值的误差界限(margin of error)(Moore, 2009)。对于异速分析而言,标度指数的误差界限可以根据参数标准误差和显著性水平计算出来。样本规模主要影响参数的误差界限,而不会影响模型的置信判断。以式(7)为例,标度指数约为b=0.8605,基于0.05的显著性水平,误差界限为0.6336到1.0764;基于0.01的显著性水平的误差界限为0.4643到1.2567。可见显著性水平越低,误差界限就会越宽。由于样本较少,标度指数估计值的误差范围就会过大。但是,就参数的可靠程度而言,相应的P值为0.0011,置信度高达99.89%。也就是说,至少有99.89%的把握判断,基于1949-2004年的5个数据点的异速生长模型及其标度指数可以接受。更简单地,可以根据相关系数作出论断。举例说来,如果相关系数大于0.8783,则置信度大于95%;如果相关系数大于0.9587,则置信度大于99%。其余依此类推。上述建模结果的置信度都在99%以上。
本文的优点也十分明显:①数据来源可靠,质量远远优于一般的统计数据(陈彦光, 2012b)。②样本点虽少,但涉及的时间跨度长达56年,这在一定程度上弥补了样本少的缺陷。因此,数学模型及其参数值都没有表现出显著的矛盾或者悖理之处。实际上,科学史上的一些规律最初就是基于小样本发现的,例如关于集成电路发展的Moore定律,开始提出时仅仅采用了4个数据点作为支持,后来的大量研究表明,Moore定律的数学表达没有问题,只是参数值存在误差（Arbesman, 2012）。③本文根据信阳观测数据开展的城市人—地异速标度关系探讨,其结论具有普遍性。

5 结论

本文主要基于城市人口、城区面积指数生长和Logistic生长的早期阶段展开分析。对于全局Logistic生长,异速标度关系更为复杂,标度指数的定义也不再简明,限于篇幅,不多讨论。可以看出,城市演化服从一般规律,但人文规律不像经典物理学定律那般严格,可能因人为因素而受到破坏(陈彦光, 2009b)。另外,人文地理的规律破坏之后会导致一系列不良后果。总之,地理科学是演化的科学,而不是存在的科学;地理规律是弹性,而不是刚性的规律(Chen, 2014b)。本文的主要结论如下:
(1) 信阳城市人口—城区面积长期服从异速标度律,且标度指数值处于合理区间。这说明中国的城市增长受到自组织演化机制的支配,否则不可能表现出显著的异速标度特征。在房地产泡沫激发“造城运动”之前的1949-2004年的50多年间,信阳城市人—地关系长期维持一种异速生长关系,这是世界各地城市普遍遵循的规律。标度指数约为0.86,处于2/3~1的合理范围内,并且接近于理论预期的0.85。这表明,在很长时间内,信阳的城市增长符合城市演化规律。
(2) 城市人地异速标度关系在2004年之后突然中断,中断的原因是羊山新区的建设。由于种种复杂的原因,中国的房地产业迅速崛起,各地“造城运动”此起彼伏,冒进城市化应运而生。在此背景下,信阳建设了羊山新区,城市面积骤然扩大。由于城市用地面积快速扩张,而人口城市化却跟不上步伐,城市人—地相互作用背后的比例关系遭到破坏,异速标度在2004-2013年间发生断裂。
(3) 标度间断导致城市用地增长难以预测,并且给未来城市发展留下隐患。城市用地过度增长不仅会导致土地资源的浪费,也将引发一系列经济社会问题,直接影响城市的可持续发展。虽然最近几年信阳城市用地大量透支,但从长远看,必然向合理的数值回归。由于土地资源的限制,将来只有通过旧城改造才能合理分配资源,调整城市人—地关系。但是,目前城市多是“见缝插针”式地建设,“摊大饼”式地扩展,旧城改造将非常困难。信阳城市建设模式不仅过早地消耗了宝贵的土地资源,而且为今后城市生活和旧城改建带来了大量隐患。
致谢:中国城市规划设计研究院的同行提供了信阳城市人口和建设用地数据,在此表示感谢。

The authors have declared that no competing interests exist.

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
陈彦光.2002. 城市人口—城区面积异速生长模型的理论基础、推广形式及其实证分析. 华中师范大学学报: 自然科学版, 36(3): 375-380.

Chen Y G.2002. The allometric models on the relationships between area and population of urban systems. Journal of Central China Normal University: Natural Science, 36(3): 375-380.

[2]
陈彦光.2008. 三个城市地域概念辨析. 城市发展研究, 15(2): 81-84, 116.

Chen Y G.2008. Distinguishing three spatial concepts of cities by using the idea from system science. Urban Development Studies, 15(2): 81-84, 116.

[3]
陈彦光.2009a. 人口与资源预测中Logistic模型承载量参数的自回归估计. 自然资源学报, 24(6): 1105-1113.

Chen Y G.2009a. Carrying capacity estimation of logistic model in population and resources prediction by nonlinear autoregression. Journal of Natural Resources, 24(6): 1105-1113.

[4]
陈彦光.2009b. 对称性与人文地理系统的规律性. 地理科学进展, 28(2): 312-320.

Chen Y G.2009b. New way of looking at human geographical laws using the idea from symmetry. Progress in Geography, 28(2): 312-320.

[5]
陈彦光.2010. 基于Excel的地理数据分析. 北京: 科学出版社.

Chen Y G.2010. Geographical data analysis using Excel. Beijing, China: Scientific Press.

[6]
陈彦光.2012a. 基于Matlab的地理数据分析. 北京: 高等教育出版社.

Chen Y G.2012a. Geographical data analysis with Matlab. Beijing, China: Higher Education Press.

[7]
陈彦光.2012b. 中国城市化水平统计数据的问题分析. 现代城市研究, 27(7): 4-8.

Chen Y G.2012b. On the enigma of China's level of urbanization. Modern Urban Research, 27(7): 4-8.

[8]
陈彦光.2013. 城市异速标度研究的起源、困境和复兴. 地理研究, 32(6): 1033-1045.

Chen Y G.2013. The rise, fall, and revival process of allometric scaling analysis in urban studies. Geographical Research, 32(6): 1033-1045.

[9]
陈彦光, 许秋红. 1999. 区域城市人口—面积异速生长关系的分形几何模型. 信阳师范学院学报: 自然科学版, 12(2): 198-203.

Chen Y G, Xu Q H.1999. Studies on the fractal geometric model of allometric growth relationships between area and population of urban systems. Journal of Xinyang Teachers College: Natural Science Edition, 12(2): 198-203.

[10]
陈彦光, 余斌. 2004. 异速生长律与城市郊区化的分维刻画. 华中师范大学学报: 自然科学版, 38(3): 370-373, 378.

Chen Y G, Yu B.2004. The law of allometric growth and theoretical foundation of several suburbanization models. Journal Of Central China Normal University: Natural Science, 38(3): 370-373, 378.

[11]
陈彦光, 周一星. 2001. 基于RS数据的城市系统异速生长分析和城镇化水平预测模型: 基本理论与应用方法. 北京大学学报: 自然科学版, 37(6): 819-826.

Chen Y G, Zhou Y X.2001. Researches on models of allometric analysis of urban systems and forecast of urbanization level based on RS data of urban area. Acta Scientiarum Naturalium Universitatis Pekinensis, 37(6): 819-826.

[12]
李郇, 陈刚强, 许学强. 2009. 中国城市异速增长分析. 地理学报, 64(4): 399-407.

Li X, Chen G Q, Xu X Q.2009. Urban allometric growth in China: theory and facts. Acta Geographica Sinica, 64(4): 399-407.

[13]
梁进社, 王旻. 2002. 城市用地与人口的异速增长和相关经验研究. 地理科学, 22(6): 649-654.

Liang J S, Wang M.2002. The allometric growth of urban land use and population and its experiential research. Scientia Geographica Sinica, 22(6): 649-654.

[14]
刘继生, 陈彦光. 2000. 长春地区城镇体系时空关联的异速生长分析: 1949-1988. 人文地理, 15(3): 6-12.

Liu J S, Chen Y G.2000. An allometric analysis of the Changchun system of towns: 1949-1988. Human Geography, 15(3): 6-12.

[15]
刘继生, 陈彦光. 2004. 城市密度分布与异速生长定律的数理关系探讨. 东北师范大学学报: 自然科学版, 36(4): 139-148.

Liu J S, Chen Y G.2004. The spatial complexity of the law of allometric growth and urban population density. Journal of Northeast Normal University: Natural Science Edition, 36(4): 139-148.

[16]
刘继生, 陈彦光. 2005. 山东省城市人口—城区面积的异速生长特征探讨. 地理科学, 25(2): 135-141.

Liu J S, Chen Y G.2005. An allometric analysis of the Shandong urban system using ideas from fractals. Scientia Geographica Sinica, 25(2): 135-141.

[17]
赵岑, 冯长春. 2010. 我国城市化进程中城市人口与城市用地相互关系研究. 城市发展研究, 17(10): 113-118.

Zhao C, Feng C C.2010. Research on the interrelation between urban land use and population in urbanization process of China. Urban Development Studies, 17(10): 113-118.

[18]
周一星.1999. 城市地理学. 北京: 商务印书馆.

Zhou Y X.1999. Urban geography. Beijing, China: The Commercial Press.

[19]
Arbesman S.2012. The half-life of facts: why everything we know has an expiration date. New York, NY: Penguin Group.

[20]
Batty M, Longley P A.1994. Fractal cities: a geometry of form and function. London, UK: Academic Press.

[21]
Bertalanffy L von.1968. General system theory: foundations, development, and applications. New York, NY: George Breziller.

[22]
Carroll C.1982. National city-size distributions: what do we know after 67 years of research? Progress in Human Geography, 6(1): 1-43.

[23]
Chen Y G.2010. Characterizing growth and form of fractal cities with allometric scaling exponents. Discrete Dynamics in Nature and Society, Volume 2010, Article ID 194715, 22 pages.

[24]
Chen Y G.2014a. An allometric scaling relation based on logistic growth of cities. Chaos, Solitons & Fractals, 65: 65-77.

[25]
Chen Y G.2014b. Multifractals of central place systems: models, dimension spectrums, and empirical analysis. Physica A: Statistical Mechanics and its Applications, 402: 266-282.

[26]
Knox P L, Marston S A.2009. Places and regions in global context: human geography (5th ed). Upper Saddle River, NJ: Prentice Hall.

[27]
Lee Y.1989. An allometric analysis of the US urban system: 1960-80. Environment and Planning A, 21(4): 463-476.

[28]
Lo C P.2002. Urban indicators of China from radiance-calibrated digital DMSP-OLS nighttime images. Annals of the Association of American Geographers, 92(2): 225-240.

[29]
Lo C P, Welch R.1977. Chinese urban population estimates. Annals of the Association of American Geographers, 67(2): 246-253.

[30]
Moore D S.2009. Statistics: concepts and controversies (7th ed). New York, NY: W H Freeman and Company.

[31]
Naroll R S, Bertalanffy L von.1956. The principle of allometry in biology and social sciences. General Systems Yearbook, 1: 76-89.

[32]
Rubenstein J M.1999. The cultural landscape: an introduction to human geography (6th ed). New York, NY: Macmillan Publishing Company.

Options
文章导航

/

〈 〉