基于功率谱周期和去趋势波动分析的河川径流特性分析

引用本文

李勋贵, 胡啸, 魏霞. .基于功率谱周期和去趋势波动分析的河川径流特性分析.自然资源学报, 2015,30(6): 986-995
LI Xun-gui, HU Xiao, WEI Xia. .Runoff Characteristics Analysis Based on Power Spectrum Method and Detrended Fluctuation Analysis.Journal of Natural Resources,2015,30(6): 986-995 复制到剪切板

Permissions

《自然资源学报》编辑部所有

基于功率谱周期和去趋势波动分析的河川径流特性分析

李勋贵, 胡啸, 魏霞

兰州大学资源环境学院,兰州 730000

第一作者简介：李勋贵（1978- ）,男,广西北流人,副教授,主要从事人类活动影响和水文水资源研究。E-mail: lixung@lzu.edu.cn

收稿日期:2014-04-08 网络出版日期:2015-06-20

基金:国家自然科学基金项目（51109103）.兰州大学中央高校基本科研业务费专项资金项目（lzujbky-2014-126,lzujbky-2015-149）

摘要

周期性和长程相关性是河川径流序列演变和波动的重要特性。论文以泾河流域杨家坪、雨落坪和张家山三个水文站1956—2001年天然径流序列为研究对象,采用功率谱周期和去趋势波动分析方法对天然径流序列进行分析,结果表明：① 张家山、杨家坪和雨落坪站的天然径流序列均为“白噪声”过程,且具有0.05置信水平下显著的2.2 a周期,径流量与降水量有较好的相关性;② 三个水文站的天然径流具有相同的标度不变区间（τ介于6~30个月）,标度指数α分别为0.549 3（张家山）、0.555 2（雨落坪）、0.554 9（杨家坪）,均大于0.5,表明三个水文站的天然径流具有长程相关性（持久性）,可能影响着径流2.2 a显著周期的形成。

关键词: 径流周期性; 长程相关性; 功率谱分析方法; 去趋势波动分析方法; 泾河流域

中图分类号:P333.1;TV121⁺.4 文献标志码:A 文章编号:1000-3037(2015)06-0986-10

Runoff Characteristics Analysis Based on Power Spectrum Method and Detrended Fluctuation Analysis

LI Xun-gui, HU Xiao, WEI Xia

College of Earth and Environmental Sciences, Lanzhou University, Lanzhou 730000, China

Abstract

Periodicity and long-range correlation are two important characteristics of the evolution and fluctuation of runoff series. This study took the natural runoff sequences over the period of 1956-2001 at three hydrologic stations (Yangjiaping, Yuluoping and Zhangjiashan) in the Jinghe Watershed as research objects. The power spectrum method and the detrended fluctuation analysis were employed to analyze the natural runoff sequences at the three stations. Results demonstrate that all of the natural runoff sequences from the three stations are “white noise” processes. Under the 0.05 confidence level, there exists a prominent period of 2.2 years for the natural sequences from the three stations. There is a good correlation between the runoff series and the precipitation. The natural runoff sequences at the three stations have the same scale invariant interval (the variable τ is between 6 and 30 months). The related scaling exponents α are greater than 0.5 (0.5493 for Zhangjiashan Station, 0.5552 for Yuluoping Station, and 0.5549 for Yangjiaping Station), which shows that there is long-range correlation or persistence of the natural runoff at the three stations. The long-range correlation may associate with the formation of 2.2-year prominent period of natural runoff sequences.

Keyword: runoff periodicity; long-range correlation; power spectrum method; detrended fluctuation analysis; Jinghe Watershed

Show Figures

河川径流的演变和波动是一种复杂的自然现象^{[1, 2, 3]}, 具有多尺度（周期）的特性^{[4, 5]}, 其对水利工程的规划、设计和运行具有重要影响^[6]。目前对时间序列周期的常用分析方法有小波分析、方差分析、功率谱周期分析等方法, 其中小波分析是一种时频分析方法, 可灵活地对平稳或非平稳数据信号进行处理^[7], 但由于小波函数不具有唯一性, 采用不同的小波基分析同一问题时会产生不同的结果^[8]; 方差分析法在识别序列的周期时, 会涉及到置信水平α 的选取问题, 如果置信水平α 选取得太高可能会得不到理想的周期个数^[9]; 功率谱周期方法是分析时间序列常用的方法, 它通过快速傅里叶变换研究频率与自相关函数的傅氏变换之间的关系, 根据功率谱图的特点直观地揭示出离散数据序列的周期性^[10], 可快速、准确地识别出径流序列的周期性。本研究采用功率谱周期方法进行分析。

河川径流序列的演变和波动的另一个重要特性为长程相关性（持久性）^[11]。时间序列的持久性特征是序列自身所固有的长期波动特征, 与序列的外在趋势不同。外在趋势往往由于受到一些外力的影响, 使时间序列表现出缓慢的单调变化或单摆波动特征, 从而在一定的时期内偏离自身固有的波动特性。传统域重新标度（R/S）分析方法在处理此情况时无能为力。另外当时间序列包含短期记忆或序列存在不均一性时, R/S分析方法往往会得出不准确的Hurst指数。为此, 20世纪90年代一些学者根据DNA机理提出了一种全新的时间序列波动长程相关性的标度指数计算方法— — 去趋势波动分析方法（Detrended Fluctuation Analysis, DFA）^[12], 随后在自然科学和社会科学等领域得到了广泛的应用, 取得了重要的研究进展。与R/S分析方法相比, DFA可以将不同阶（1~p阶）的外在趋势从原有序列中剔除, 从而结果更加真实、可靠, 优于R/S分析法^[13]。

泾河为渭河的一级支流、黄河的二级支流, 具有十分重要的区位优势。杨家坪、雨落坪和张家山水文站分别为泾河干流上游区、马莲河（泾河最大支流）和整个流域的把口站, 控制流域面积分别为14 124、19 019、43 216 km²。目前在泾河径流的特性分析方面, 主要集中于径流的趋势或周期演变分析^{[14, 15, 16, 17, 18]}以及分形特性分析^[19]等方面, 如李雯分析了泾河流域张家山站年径流量的年际变化和年内变化特征^[14]; 李勋贵采用Mann-Kendall方法分析了泾河流域杨家坪、雨落坪和张家山站径流序列的变化趋势^[15]; 吕静渭采用滑动平均法和Kendall秩次相关检验法分析了泾河流域年径流量的变化趋势, 并基于小波分析研究了年径流量的变化周期^[16]; 陈晨等采用Morlet小波对泾河流域1932— 2010年的实测径流序列的周期、丰枯变化及突变点进行了分析^[18]; 陈刚等基于分形理论和GIS技术对1932— 1999年泾河张家山水文站1日、7日和15日径流的分形特征进行了研究^[19]。尽管当前研究在泾河流域径流特性分析方面取得了重要研究进展, 但仍鲜见有周期性以及长程相关性方面的综合报道, 这不利于流域河川径流特性的进一步揭示。因此, 采用有效的方法来探讨河川径流的演变和波动特性具有十分重要的科学意义和应用价值。本研究基于功率谱周期和去趋势波动分析方法, 对泾河杨家坪、雨落坪和张家山水文站天然径流序列的周期性和长程相关性进行分析, 并探讨其成因, 这对于分析泾河流域径流系统波动规律及其演变特性具有重要的意义。

1 理论方法

1.1 功率谱周期分析方法

预先给定离散时间序列为 $\begin{matrix} Y (t) \end{matrix}$ $\begin{matrix} (t = 1, 2, \dots, n) \end{matrix}$ , 功率谱周期分析方法步骤如下：

1）数据序列标准化处理。设序列 $\begin{matrix} Y (t) \end{matrix}$ 的均值和标准差分别为μ _y和为σ _y, 则标准化后的新序列为： $\begin{matrix} \overset{′}{y} (t) = [Y (t) - μ_{y}] / σ_{y} (t = 1, 2, \dots, n) \end{matrix}$ 。

2）计算序列的自相关函数：

$\begin{matrix} r (τ) = \frac{1}{n - τ} \overset{n - τ}{\sum_{t = 1}} \overset{′}{y} (t) \overset{′}{y} (t + τ) (τ = 0, 1, 2, ∙ ∙ ∙, m) \end{matrix}$ （1）

式中：τ 为自相关函数的时延; m为最大时延, 本研究中, 当 $\begin{matrix} n \geq 50 \end{matrix}$ 时, 取 $\begin{matrix} m = n / 10 \end{matrix}$ , 当 $\begin{matrix} n ＜ 50 \end{matrix}$ 时, 取 $\begin{matrix} m = n / 4 \end{matrix}$ 。

3）计算不同时延的粗估谱：

$\begin{matrix} E (k) = \frac{1}{m} \{r (0) + 2 \overset{m - 1}{\sum_{τ = 1}} r (τ) \cos \frac{kπ}{m} τ + r (m) coskπ\} (k = 0, 1, 2 ∙ ∙ ∙, m) \end{matrix}$ （2）

式中： $\begin{matrix} k \end{matrix}$ 为谐波波数。 $\begin{matrix} E (k) \end{matrix}$ 一般随 $\begin{matrix} k \end{matrix}$ 值的变化起伏较大, 需要对其作平滑处理：

$\begin{matrix} \tilde{E} (k) = \{\begin{matrix} 0.54 E (k) + 0.46 E (k + 1) (k = 0) \\ 0.23 E (k - 1) + 0.54 E (k) + 0.23 E (k + 1) (1 \leq k < m) \\ 0.46 E (k - 1) + 0.54 E (k) (k = m) \end{matrix} \end{matrix}$ （3）

4）周期分析。以 $\begin{matrix} k \end{matrix}$ 为横坐标、精细谱 $\begin{matrix} \tilde{E} (k) \end{matrix}$ 为纵坐标绘制功率谱图。根据图形的极大值确定序列的周期 $\begin{matrix} T_{k} = 2 m / k \end{matrix}$ 。

5）周期检验。假设样本的总体谱密度为随机过程谱密度, 谱估计（χ ²分布检验）的自由度为 $\begin{matrix} ζ = (2 n - 3 m / 2) / m \end{matrix}$ , 则精细谱估计 $\begin{matrix} \tilde{E} (k) \end{matrix}$ 与其平均值 $\begin{matrix} \overset{̅}{E} (k) \end{matrix}$ 之比呈 $\begin{matrix} \frac{χ^{2}}{ζ} \end{matrix}$ 分布, 即： $\begin{matrix} \tilde{E} (k) \end{matrix}$ / $\begin{matrix} \overset{̅}{E} (k) \end{matrix}$ = $\begin{matrix} \frac{χ^{2}}{ζ} \end{matrix}$ 。

平均谱估计值 $\begin{matrix} \overset{̅}{E} (k) \end{matrix}$ 的计算与随机过程的性质有关。如果式（1）的自相关函数r(1)为较大正值, 表明序列为“ 红噪声” ; 若r(1)接近零或为负值时, 表明序列为“ 白噪声” 。“ 红噪声” 和“ 白噪声” 的 $\begin{matrix} \overset{̅}{E} (k) \end{matrix}$ 分别如式（4）和式（5）所示：

$\begin{matrix} \overset{̅}{E} (k) = [\frac{1 - r^{2} (1)}{1 + r^{2} (1) - 2 r (1) \cos \frac{kπ}{m}}] \{\frac{1}{2 m} [\tilde{E} (0) + \tilde{E} (m)] + \frac{1}{m} \overset{m - 1}{\sum_{k = 1}} \tilde{E} (k)\} \end{matrix}$ （4）

$\begin{matrix} \overset{̅}{E} (k) = \frac{1}{2 m} [\tilde{E} (0) + \tilde{E} (m)] + \frac{1}{m} \overset{m - 1}{\sum_{k = 1}} \tilde{E} (k) \end{matrix}$ （5）

如果关系 $\begin{matrix} \tilde{E} (k) \end{matrix}$ > ( $\begin{matrix} \frac{{χ_{α}}^{2}}{ζ} \end{matrix}$ ) $\begin{matrix} \overset{̅}{E} (k) \end{matrix}$ 成立, 则表明 $\begin{matrix} \tilde{E} (k) \end{matrix}$ 以α 显著水平不接受 $\begin{matrix} \tilde{E} (k) \end{matrix}$ 为非周期谱值。其中 $\begin{matrix} χ_{0.05}^{2} \approx ζ + 0.85 + 1.645 \sqrt[]{2 ζ - 1} \end{matrix}$ , $\begin{matrix} χ_{0.01}^{2} \approx ζ + 2.20 + 2.326 \sqrt[]{2 ζ - 1} \end{matrix}$ 。

1.2 去趋势波动分析方法

1）设具有非平稳的时间序列为 $\begin{matrix} {x (t), t = 1, 2, \dots, N} \end{matrix}$ , 对 $\begin{matrix} x (t) \end{matrix}$ 求累积和, 形成一个累积序列 $\begin{matrix} \begin{matrix} y (k) = \overset{k}{\sum_{t = 1}} [x (t) - \overset{̅}{x}] & (k = 1, 2, \dots, N) \end{matrix} \end{matrix}$ , $\begin{matrix} \overset{̅}{x} \end{matrix}$ 为 $\begin{matrix} x (t) \end{matrix}$ 的均值。

2）将 $\begin{matrix} y (k) \end{matrix}$ 平分成 $\begin{matrix} M (= N / τ) \end{matrix}$ 个长度为 $\begin{matrix} τ \end{matrix}$ 的不重叠区间, $\begin{matrix} y (k) \end{matrix}$ 中不能被τ 整除的部分可以忽略不计。假设每个区间均具有一个与时间t有关的p阶趋势, 则有区间趋势方程 $\begin{matrix} y_{τ} (k) = \overset{p}{\sum_{j = 0}} β_{j} t^{j} \end{matrix}$ , 参数 $\begin{matrix} β_{j} (j = 0, 1, 2, \dots, p) \end{matrix}$ 由区间数据的最小二乘拟合得到;

3）对每一区间进行去趋势处理, 即： $\begin{matrix} Δ y_{τ} (k) = y (k) - y_{τ} (k) \end{matrix}$ ;

4）计算新的时间序列 $\begin{matrix} Δ y_{τ} (k) \end{matrix}$ 特征长度的波动：

$\begin{matrix} F (τ) = \sqrt[]{\frac{1}{N} \overset{N}{\sum_{k = 1}} [Δ y_{τ} {(k)]}^{2}} \end{matrix}$ （6）

5）变换区间尺度τ 从2到N, 重复步骤2）~4）, 得到一个 $\begin{matrix} F (τ) \end{matrix}$ 随区间尺度τ 变化的曲线;

6）分别求 $\begin{matrix} F (τ) \end{matrix}$ 和τ 的对数。如果 $\begin{matrix} \log [F (τ)] \end{matrix}$ 与 $\begin{matrix} log τ \end{matrix}$ 呈线性关系, 其斜率便是尺度（或标度）指数α , 说明 $\begin{matrix} F (τ) \end{matrix}$ 呈现自相似过程, 即：

$\begin{matrix} F (τ) ~ τ^{α} \Rightarrow F (τ) = A τ^{α} \Rightarrow \log [F (τ)] = logA + αlogτ \end{matrix}$ （7）

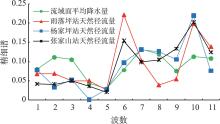
DFA的幂指数α 与Hurst指数H的意义相同。不同的尺度指数α 值反映了不同的时间过程, α 值与自相关函数有着密切的关系^{[20, 21]}：当 $\begin{matrix} 0 < α < 0.5 \end{matrix}$ 时, 序列具有短程相关性（短期记忆）; 当 $\begin{matrix} α = 0.5 \end{matrix}$ 时, 序列是自相关函数为0的随机序列; 当 $\begin{matrix} 0.5 < α < 1 \end{matrix}$ 时, 序列是一个具有持久性（长期相关性）的增强时间序列, 即在时刻t以前存在的上升或下降趋势, 在时刻t以后可能会再次出现, 其趋势增强行为取决于 $\begin{matrix} α > 0.5 \end{matrix}$ 的程度; 当 $\begin{matrix} α = 1 \end{matrix}$ 时, 序列是一个 $\begin{matrix} 1 / f \end{matrix}$ 过程; 当 $\begin{matrix} α ＝ 1.5 \end{matrix}$ , 序列是一个布朗运动过程。

2 结果与讨论

本研究选取泾河流域杨家坪、雨落坪和张家山三个水文站的月天然径流量为研究对象, 径流序列长度为1956— 2001年, 资料来自于黄河水利委员会, 还原水量通过分项还原法获得。尽管该法存在调查的年份较长、调查的数据和涉及的参数繁多、在还原时可能会引起累积误差等不足, 但其在人类活动影响较小的情况下有较高的还原精度, 在人类活动影响较大的区域, 还原成果的总体趋势不变^[22]。因此, 认为来自于黄河水利委员会的天然径流量资料是可靠的。杨家坪、雨落坪和张家山站的多年平均天然径流量分别为8.36× 10⁸、4.61× 10⁸和19.98× 10⁸ m³。图1为三个水文站天然径流量距平变化趋势。从图中可以看出, 张家山和杨家坪站丰枯变化同步的年份有42 a, 同步概率为91.30%, 张家山和雨落坪站丰枯同步的年份有37 a, 同步概率为80.43%, 而杨家坪和雨落坪站丰枯同步的年份仅有35 a, 同步概率仅为76.09%, 说明张家山和杨家坪站的丰枯同步性最好（这两个序列的相关系数达到0.85）, 而杨家坪和雨落坪站的丰枯同步性最差（相关系数仅为0.50）, 这是由于这两个测站之间没有水力联系, 非上下游关系。

	Figure Option View Download New Window
	图1 泾河流域杨家坪、雨落坪和张家山水文站天然年径流量距平变化过程Fig. 1 Anomaly changings of annual natural runoffs at Yangjiaping, Yuluoping and Zhangjiashan stations in the Jinghe Watershed

通过Mann-Kendall（MK）方法对径流趋势的进一步分析, 结果（如图2所示）发现：杨家坪站的年、汛期和非汛期径流量的MK统计量均小于零, 且通过0.01的置信水平检验, 呈现出极显著的递减趋势; 雨落坪站除汛期径流量呈现出不显著的递增趋势之外, 年径流量和非汛期径流量均呈现出递减趋势, 而后者的递减趋势通过0.1的置信水平检验, 递减趋势显著; 张家山站年、汛期和非汛期径流量均呈现出递减趋势, 其中年径流量和汛期径流量的递减趋势通过0.01的置信水平检验, 递减趋势极显著。这表明, 采用DFA方法计算序列的长程相关性时, 需要对序列进行去趋势化处理。

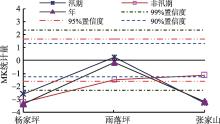	Figure Option View Download New Window
	图2 泾河流域杨家坪、雨落坪和张家山站天然径流序列MK趋势检验结果Fig. 2 Mann-Kendall tendency test for annual natural runoffs at Yangjiaping, Yuluoping and Zhangjiashan stations in the Jinghe Watershed

2.1 径流功率谱周期性结果与讨论

根据功率谱周期分析方法, 对泾河流域面平均降水量以及张家山、杨家坪和雨落坪水文站天然径流量进行功率谱周期分析, 结果如表1和图3所示。

表1 泾河流域张家山、杨家坪和雨落坪水文站天然径流序列功率谱分析结果 Table 1 Power spectrum analysis results of annual natural runoffs at Zhangjiashan, Yangjiaping and Yuluoping stations in the Jinghe Watershed

	Figure Option View Download New Window
	图3 泾河流域面平均降水量和张家山、杨家坪、雨落站水文站天然径流序列功率谱图Fig. 3 Power spectrum changings of the annual natural runoffs at Zhangjiashan, Yangjiaping and Yuluoping hydrological stations and the annual areal precipitation in the Jinghe Watershed

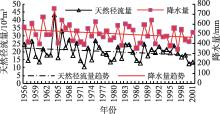从表1可以看出, 张家山、杨家坪和雨落坪站的自相关函数 $\begin{matrix} r (1) \end{matrix}$ 分别为-0.361、-0.290和-0.221, 均小于零, 三水文站的天然径流序列均为“ 白噪声” 过程, 故采用式（5）来计算平均谱估计值 $\begin{matrix} \overset{̅}{E} (k) \end{matrix}$ 。从图3可知, 当张家山站在波数 $\begin{matrix} k = 6 \end{matrix}$ 和10、杨家坪站在波数 $\begin{matrix} k = 7 \end{matrix}$ 和10、雨落坪站在波数 $\begin{matrix} k = 6 \end{matrix}$ 和10时, 精细谱有极大值, 这表明径流存在着与这些波数对应的周期。对照表1可知, 张家山站具有3.7和2.2 a的周期, 杨家坪站有3.1和2.2 a的周期, 雨落坪站有3.7和2.2 a的周期, 共同周期为2.2 a, 且该周期在0.05置信水平下是显著的, 雨落坪站的3.7 a周期在0.05置信水平下亦是显著的。其他研究者^{[16, 17, 18]}也指出泾河流域年径流具有2或3 a的变化周期, 与本文的研究结果相一致。从图3还可以看出, 在波数 $\begin{matrix} k = 7 \end{matrix}$ 和10时, 流域降水量的精细谱存在极大值, 这表明流域降水量存在着3.1和2.2 a的变化周期, 与文献[14]和[16]分别采用功率谱周期和小波分析方法得到的4.3和3 a不显著周期结果较为接近。

	Figure Option View Download New Window
	图4 泾河张家山以上流域降水量和张家山站天然径流量过程线Fig. 4 Relationship between annual precipitation and natural runoff of Zhangjiashan station in the Jinghe Watershed

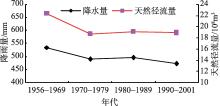	Figure Option View Download New Window
	图5 泾河张家山以上流域降水量和张家山站天然径流量各年代变化过程Fig. 5 Relationship between precipitation and natural runoff of Zhangjiashan station during different periods in the Jinghe Watershed

通过对径流量与降水量关系的分析, 结果（如图4、5所示）表明：张家山站径流量的变化趋势与其控制流域降水量的变化趋势有较好的对应关系, 两者的相关系数为0.784, 绝对值大于径流量与气温的相关系数（-0.439）和径流量与蒸发量的相关系数（-0.519）, 这说明流域降水量的变化是影响天然径流量变化的主要因子。尽管杨家坪站以上流域来水对张家山站的径流贡献最大、相关性最好（图1）, 但从图3可以看出, 这两站的径流周期并不完全同步, 这说明径流周期的形成是一个复杂的过程。泾河流域位于黄河中游地区, 受到来自西太平洋副热带高压、青藏高原高度场以及印度槽的综合影响^[23], 流域降水量和径流量序列中存在的2.2 a周期可能与气候系统中的海-气相互作用的准2 a振荡周期^{[24, 25]}以及厄尔尼诺事件的2~4 a变化周期^[26]有关; 而降水量的3.1 a周期以及径流量的3.1和3.7 a周期的变化可能与厄尔尼诺事件的2~4 a变化周期^[26]以及副高脊线位置的3 a准周期^{[27, 28, 29, 30]}有关。

	Figure Option View Download New Window
	图6 泾河流域张家山、雨落坪和杨家坪站天然径流序列长程相关性结果Fig. 6 Long-range correlation of the natural runoff sequences at Zhangjiashan, Yuluoping and Yangjiaping stations in the Jinghe Watershed

2.2 径流长程相关性结果与讨论

基于去趋势波动分析方法, 可以获得如图6和表2所示的天然径流序列长程相关性结果。从图6中可以看出, 张家山、雨落坪和杨家坪站径流的长程相关性变化趋势类似, 张家山、雨落坪和杨家坪站的 $\begin{matrix} logF (τ) \end{matrix}$ 存在着0.01置信水平下显著相关的线性函数, 分别为：y=0.549 3x+5.698 6 (R²=0.585 6)、y=0.555 2x+5.678 0 (R²=0.579 6)、y=0.554 9x+5.679 1 (R²=0.580 0)。由表2可以看出, 张家山、雨落坪和杨家坪站天然径流量具有相同的标度不变区间, 即τ 均介于6~30个月; 标度指数α 也很接近, 分别为0.549 3、0.555 2和0.554 9, 均大于0.5, 表明三个站点的天然径流序列具有长程相关性（持久性）, 即如果当前时期径流为丰（或枯）, 那么下一个时期径流为丰（或枯）的可能性会更大。本研究所得的张家山站的标度指数α 值与周安康^[31]采用1960— 1995年值计算所得结果（0.589）较为接近。同时, 周安康^[31]还获得渭河干流的咸阳站、华县站和北洛河的状头站的标度指数α 值分别为0.626、0.622和0.639, 值亦大于0.5, 说明渭河流域中下游地区径流表现出类似的长程相关性。同时, 李鹏和赵雪花^[32]得到1956— 2000年汾河流域兰村站的标度指数a为0.553 2, 佟春生等^[33]采用DFA方法获得1920— 2003年黄河流域下游花园口水文站的标度指数α 值为0.568 8。本文和这些研究成果在一定程度上说明, 包括渭河的两大支流泾河和洛河、汾河在内的黄河中下游地区的径流序列可能表现出类似的长程相关性。

有研究表明, 泾河流域径流波动的这种持久性（长程相关性）, 与径流系统的复杂性有一定联系^[34]。由表2可知, 当张家山、雨落坪和杨家坪站的天然径流序列的区间尺度τ 介于6~30个月时, 满足标度不变性特征, 具有统一的持久性波动特征, 即三个站点天然径流的长程相关性均为6~30个月（0.5~2.5 a）。这表明当某月出现某次洪峰过程时, 在其后的6~30个月内很有可能会出现类似的洪峰过程。另外, 从表1可知, 张家山、雨落坪和杨家坪站天然径流量具有2.2 a显著周期, 介于0.5~2.5 a之间, 故可认为2.2 a的显著周期为天然径流固有的波动特征, 而3.1或3.7 a周期可能是外力作用下（如厄尔尼诺、南方涛动等^{[35, 36, 37]}）使2.2 a固有周期呈现的一种变形周期。这表明径流所具有的周期性与其自身的长程相关性有一定的联系, 径流的周期性是其自身长程相关性的外在表现形式。

表2 泾河流域张家山、雨落坪和杨家坪站天然径流序列的标度指数及其不变区间 Table 2 Scaling exponents and invariant intervals of the natural runoff sequences at Zhangjiashan, Yuluoping and Yangjiaping stations in the Jinghe Watershed

3 结论

本研究采用功率谱周期和去趋势波动分析方法（Detrended Fluctuation Analysis, DFA）对泾河流域张家山、杨家坪和雨落坪水文站1956— 2001年的月天然径流序列的周期性和长程相关性进行了分析, 取得如下主要研究结论：

（1）张家山、杨家坪和雨落坪站的天然径流序列均为“ 白噪声” 过程。三个水文站的径流具有在0.05置信水平下2.2 a的显著周期, 雨落坪站的3.7 a周期在0.05置信水平下亦是显著的, 但杨家坪站的3.1 a周期和张家山站的3.7 a周期在该置信水平下并不显著。流域径流的周期性受到多种复杂因素的共同影响, 径流量与降水量有较好的相关性。

（2）张家山、雨落坪和杨家坪站的天然径流序列具有相同的标度不变区间, 即τ 分别介于6~30个月, 这表明当某月出现某次洪峰过程时, 在其后的6~30个月（0.5~2.5 a）内很有可能会出现类似的洪峰过程。三个水文站的标度指数α 分别为0.549 3、0.555 2和0.554 9, 均大于0.5, 表明天然径流具有长程相关性（持久性）。这些站点的天然径流具有0.05置信水平下的2.2 a显著周期, 可能是泾河天然径流固有的波动特征, 而3.1或3.7 a周期可能是外力作用下使2.2 a固有周期呈现的一种变形周期。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Perrier V, Philipovitch T, Basdevant C. Wavelet spectra compared to Fourier Spectral[J]. Journd of Mathematicd Physics, 1995, 36(3): 1506-1519. [本文引用:1]
[2]	黄忠恕. 波普分析方法及其在水文气象学中的应用 [M]. 北京: 气象出版社, 1983. [HUANG Zhong-shu. Spectrum Analysis and Its Applications to Hydrometeorology. Beijing: China Meteorological Press, 1983. ] [本文引用:1]
[3]	衡彤. 小波分析及其应用研究[D]. 成都: 四川大学, 2003. [HENG Dong. Wavelet Analysis and Its Application. Chengdu: Sichuan University, 2003. ] [本文引用:1]
[4]	Li J Z, Feng P. Runoff variations in the Luanhe River Basin during 1956-2002[J]. Journal of Geographical Sciences, 2007, 17(3): 339-350. [本文引用:1] [JCR: 1.123] [CJCR: 0.81]
[5]	王文圣, 丁晶, 向红莲. 水文时间序列多时间尺度分析的小波变换法[J]. 四川大学学报: 工程科学版, 2002, 34(6): 14-17. [WANG Wen-sheng, DING Jing, XIANG Hong-liang. Multiple time scales analysis of hydrological time series with wavelet transform. Journal of Sichuan University : Engineering Science Edition, 2002, 34(6): 14-17. ] [本文引用:1] [CJCR: 0.1927]
[6]	王义民. 梯级水库洪水调度模式研究——以黄河上游梯级水库防洪调度为例 [D]. 西安: 西安理工大学, 2004. [WANG Yi-min. Flood Operation Mode of Cascade Reservoirs-with Cascade Reservoirs Flood Operation in Upper Reaches of the Yellow River as an Example . Xi’an: Xi’an University of Technology, 2004. ] [本文引用:1]
[7]	Kang S, Lin H. Wavelet analysis of hydrological and water quality signals in an agricultural watershed[J]. Journal of Hydrology, 2007, 338(1-2): 1-14. [本文引用:1] [JCR: 2.693]
[8]	蔡棋瑛, 林建华. 基于小波分析和神经网络的桩身缺陷诊断[J]. 振动与冲击, 2002, 21(3): 11-17. [CAI Qi-ying, LIN Jian-hua. Pile defect diagnosis based on wavelet analysis and neural networks. Journal of Vibration and Shock, 2002, 21(3): 11-17. ] [本文引用:1] [CJCR: 0.782]
[9]	曲静, 王昱. 方差分析周期外推法在春季降水量预报中的应用[J]. 甘肃科学学报, 2012, 24(2): 68-71. [QU Jing, WANG Yu. Application of variance analysis and extrapolation method to forecasts of spring precipitation. Journal of Gansu Sciences, 2012, 24(2): 68-71. ] [本文引用:1] [CJCR: 0.261]
[10]	吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用 [M]. 武汉: 武汉大学出版社, 2002. [LV Jing-hu, LU Jun-an, CHEN Shi-hua. Chaos Time Sequence Analysis and Its Application. Wuhan: Wuhan University Press, 2002. ] [本文引用:1]
[11]	燕爱玲, 黄强, 王义民. 河川径流演变的非趋势波动分析[J]. 水力发电学报, 2007, 26(3): 1-4. [YAN Ai-ling, HUANG Qiang, WANG Yi-min. Detrended fluctuation analysis of river runoff evolvement. Journal of Hydroelectric Engineering, 2007, 26(3): 1-4. ] [本文引用:1] [CJCR: 0.656]
[12]	Peng C K, Buldrev S V, Goudberger A L, et al. Finite size effects on long range correlations: Implications for analyzing DNA sequences[J]. Physical Review E, 1993, 47(5): 3730-3733. [本文引用:1] [JCR: 2.326]
[13]	Weron R. Estimating long-range dependence: finite sample properties and confidence intervals[J]. Physica A, 2002, 312: 285-299. [本文引用:1] [JCR: 1.722]
[14]	李雯. 泾河流域气候变化对径流量的影响研究[D]. 西安: 长安大学, 2008. [LI Wen. Impacts of Climate Change in Jing River Basin on the Runoff. Xi'an: Chang'an University, 2008. ] [本文引用:2]
[15]	李勋贵. 水资源系统耦合理论及其在泾河水文水资源研究中的应用[D]. 西安: 长安大学, 2008. [LI Xun-gui. Theory of Water Resources System Coupling and Its Application to Study of Water Resources and Hydrology in Jinghe River. Xi'an: Chang'an University, 2008. ] [本文引用:2]
[16]	吕静渭. 泾河流域径流变化规律与预报模型研究 [D]. 杨凌: 西北农林科技大学, 2010. [Lü Jing-wei. Study on the Runoff Change Characteristic and Forecast Model in Jinghe River Basin . Yangling: Northwest A & F University, 2010. ] [本文引用:3]
[17]	吕静渭, 马孝义, 高文强, 等. 近70年来泾河年径流量周期变化的小波分析[J]. 人民黄河, 2010, 32(2): 49-50, 67. [Lü Jing-wei, MA Xiao-yi, GAO Wen-qiang, et al. Wavelet analysis of periodicity changes from annual runoff over 70 years in the Jinghe watershed. Yellow River, 2010, 32(2): 49-50, 67. ] [本文引用:2] [CJCR: 0.373]
[18]	陈晨, 罗军刚, 解建仓, 等. 泾河流域近80a径流变化趋势及特征分析[J]. 人民黄河, 2013, 35(1): 26-28, 38. [CHEN Chen, LUO Jun-gang, XIE Jian-cang, et al. Chang trend and characteristics of runoff sequences over 80 years in the Jinghe River Basin. Yellow River, 2013, 35(1): 26-28, 38. ] [本文引用:3] [CJCR: 0.373]
[19]	陈刚, 胡素端, 王怡璇, 等. 基于GIS的泾河流域径流过程分形特征研究[J]. 水资源与水工程学报, 2011, 22(3): 124-127. [CHEN Gang, HU Su-duan, WANG Yi-xuan, et al. Research on fractal characteristics of runoff process in the Jinghe River Basin based on GIS. Journal of Water Resources and Water Engineering, 2011, 22(3): 124-127. ] [本文引用:2] [CJCR: 0.418]
[20]	庄新田, 黄小原. 证券市场的标度理论及实证研究[J]. 系统工程理论与实践, 2003, 23(3): 1-8. [ZHUANG Xin-tian, HUANG Xiao-yuan. Scale theory and empirical research in the securities market. Systems Engineering-theory & Practice, 2003, 23(3): 1-8. ] [本文引用:1]
[21]	何越磊, 姚令侃, 苏凤环. 强沙尘暴时序的标度不变性分析[J]. 系统工程理论与实践, 2005, 25(7): 125-130. [HE Yue-lei, YAO Ling-kan, SU Feng-huan. Scale invariance analysis of the time series of severe sand and dust storm. Systems Engineering-theory & Practice, 2005, 25(7): 125-130. ] [本文引用:1]
[22]	李勋贵, 魏霞. 基于系统周界观控模型的径流还原方法[J]. 水利水电技术, 2015, 46(1): 11-16. [LI Xun-gui, WEI Xia. Runoff restoration method based on observability-controllablity model of periphery. Water Resources and Hydropower Engineering, 2015, 46(1): 11-16. ] [本文引用:1] [CJCR: 0.372]
[23]	张明, 张建云, 金菊良. 基于遗传熵谱估计的年径流周期识别[J]. 水科学进展, 2009, 20(3): 337-342. [ZHANG Ming, ZHANG Jian-yun, JIN Ju-liang. Genetic entropy spectral estimation method and its application to annual runoff periodic identification. Advances in Water Science, 2009, 20(3): 337-342. ] [本文引用:1] [CJCR: 1.672]
[24]	杨明金, 张勃. 黑河莺落峡站径流变化的影响因素分析[J]. 地理科学进展, 2010, 29(2): 166-172. [YANG Ming-jin, ZHANG Bo. The study on affecting factors of runoff changes at Yingluoxia Station of Heihe River. Progress in Geography, 2010, 29(2): 166-172. ] [本文引用:1] [CJCR: 1.791]
[25]	Wang H. Impact of the 11yr solar activity on the QBO in the climate system[J]. Advance in Atmospheric Sciences, 2003, 20(2): 303-309. [本文引用:1] [JCR: 1.459] [CJCR: 1.057]
[26]	Hao Z, Zhang J, Ge Q. Precipitation cycles in the middle and lower reaches of the Yellow River (1736-2000)[J]. Journal of Geographic Sciences, 2008, 18(1): 17-25. [本文引用:2]
[27]	徐国昌, 董安祥. 我国西部降水量的准三年周期[J]. 高原气象, 1982, 1(2): 11-16. [XU Guo-chang, DONG An-xiang. The quasi-three year period of precipitation in the west of China. Plateau Meteorology, 1982, 1(2): 11-16. ] [本文引用:1] [CJCR: 1.979]
[28]	梁建茵. 6月西太平洋副高脊线的年际变化及其对华南降水的影响[J]. 热带气象学报, 1994, 10(3): 274-279. [LIANG Jian-yin. The interannual variations of the subtropic high ridge position over western pacific in June and its influence on precipitation in south of China. Journal of Tropical Meteorology, 1994, 10(3): 274-279. ] [本文引用:1] [CJCR: 1.073]
[29]	赵振国, 陈国珍. 初夏西太平洋副高南北位置长期变化的成因及预报[J]. 热带气象学报, 1995, 11(3): 223-230. [ZHAO Zhen-guo, CHEN Guo-zhen. The cause and forecast of long-term change of the latitudinal position of west Pacific subtropical high in early summer. Journal of Tropical Meteorology, 1995, 11(3): 223-230. ] [本文引用:1] [CJCR: 1.073]
[30]	许金镜, 林新彬, 温珍治. 夏季副高位置的变化规律及其与福建干旱的关系分析[J]. 台湾海峡, 2005, 24(3): 363-369. [XU Jin-jing, LIN Xin-bin, WEN Zhen-zhi. Variation of subtropical high and an analysis of its relationship with drought in Fujian during summer. Journal of Oceanography in Taiwan Strait, 2005, 24(3): 363-369. ] [本文引用:1] [CJCR: 0.612]
[31]	周安康. 基于分形理论和信息熵的渭河流域生态环境状况研究[D]. 杨凌: 西北农林科技大学, 2012. [ZHOU An-kang. Research of Ecological Environment Condition based on the Fractal Theory and Information Entropy in the Wei River Basin. Yangling: Northwest A & F University, 2012. ] [本文引用:2]
[32]	李鹏, 赵雪花. 兰村站天然径流演变长程相关性分析[J]. 科技情报开发与经济, 2011, 21(30): 179-181. [LI Peng, ZHAO Xue-hua. Long-range correlation analysis on Lancun Station’s natural runoff evolution. Sci-Tech Information Development & Economy, 2011, 21(30): 179-181. ] [本文引用:1]
[33]	佟春生, 黄强, 刘涵, 等. 黄河径流序列标度不变性分析及趋势预测研究[J]. 自然资源学报, 2007, 22(4): 634-639. [TONG Chun-sheng, HUANG Qiang, LIU Han, et al. Scale invariant analysis and runoff trend prediction of the runoff time series in the Yellow River. Journal of Natural Resources, 2007, 22(4): 634-639. ] [本文引用:1] [CJCR: 1.841]
[34]	佟春生. 复杂性理论在河川径流时间序列分析中的应用研究 [D]. 西安: 西安理工大学 [ 2005. ] [TONG Chun-sheng, Application Study of Complexity Theory in River Runoff Time Series Analysis. Xi’an: Xi’an University of Technology, 2005] [本文引用:1]
[35]	Liu F, Chen S, Dong P, et al. Spatial and temporal variability of water discharge in the Yellow River Basin over the past 60 years[J]. Journal of Geographical Sciences, 2012, 22(6): 1013-1033. [本文引用:1]
[36]	李月洪, 张正秋. 百年来中国黄河流域区域性旱涝气候突变[J]. 地理科学, 1993, 13(4): 315-321. [LI Yue-hong, ZHANG Zheng-qiu, Abrupt climatic change of drought and flood in the Huanghe River Basin during the last 10years. Scientia Geographica Sinica, 1993, 13(4): 315-321] [本文引用:1] [CJCR: 2.498]
[37]	蓝永超, 马全杰, 康尔泗, 等. ENSO循环与黄河上游径流的丰枯[J]. 中国沙漠, 2002, 22(3): 262-266. ] [LAN Yong-chao, MA Quan-jie, KANG Er-si, et al, Relationship between ENSO cycle and abundant or low runoff in the upper Yellow River. Journal of Desert Research, 2002, 22(3): 262-266] [本文引用:1] [CJCR: 2.412]

1995

0.0

... 河川径流的演变和波动是一种复杂的自然现象^[1,2,3],具有多尺度（周期）的特性^[4,5],其对水利工程的规划、设计和运行具有重要影响^[6] ...

1983

0.0

... 河川径流的演变和波动是一种复杂的自然现象^[1,2,3],具有多尺度（周期）的特性^[4,5],其对水利工程的规划、设计和运行具有重要影响^[6] ...

2003

0.0

衡彤. 小波分析及其应用研究[D]. 成都: 四川大学, 2003.

[HENG

Dong

. Wavelet Analysis and Its Application. Chengdu: Sichuan University, 2003. ]

小波变换是当前应用数学和工程学科中一个迅速发展的新领域.文章介绍了小波变换的基本概念,讨论了其在各个领域的应用,最后对其发展前景进行了展望.

... 河川径流的演变和波动是一种复杂的自然现象^[1,2,3],具有多尺度（周期）的特性^[4,5],其对水利工程的规划、设计和运行具有重要影响^[6] ...

2007

1.123

0.81

... 河川径流的演变和波动是一种复杂的自然现象^[1,2,3],具有多尺度（周期）的特性^[4,5],其对水利工程的规划、设计和运行具有重要影响^[6] ...

2002

0.0

0.1927

王文圣, 丁晶, 向红莲. 水文时间序列多时间尺度分析的小波变换法[J]. 四川大学学报: 工程科学版, 2002, 34(6): 14-17.

[WANG

Wen-sheng

, DING

Jing

, XIANG

Hong-liang.

Multiple time scales analysis of hydrological time series with wavelet transform. Journal of Sichuan University :

Engineering Science Edition, 2002, 34(6): 14-17. ]

以长江宜昌站近100年(1890～1987)年平均流量过程为例,利用Marr小波和Morlet小波变换对水文序列的多时间尺度演变特性进行了分析.研究结果表明,其年际及年代际时间尺度在时间域中分布很不均匀,具有明显的局部化特征.小波变换法分析水文水资源系统多时间尺度是优越的.

... 河川径流的演变和波动是一种复杂的自然现象^[1,2,3],具有多尺度（周期）的特性^[4,5],其对水利工程的规划、设计和运行具有重要影响^[6] ...

2004

0.0

... 河川径流的演变和波动是一种复杂的自然现象^[1,2,3],具有多尺度（周期）的特性^[4,5],其对水利工程的规划、设计和运行具有重要影响^[6] ...

2007

2.693

0.0

... 目前对时间序列周期的常用分析方法有小波分析、方差分析、功率谱周期分析等方法,其中小波分析是一种时频分析方法,可灵活地对平稳或非平稳数据信号进行处理^[7],但由于小波函数不具有唯一性,采用不同的小波基分析同一问题时会产生不同的结果^[8] ...

2002

0.0

0.782

蔡棋瑛, 林建华. 基于小波分析和神经网络的桩身缺陷诊断[J]. 振动与冲击, 2002, 21(3): 11-17.

[CAI

Qi-ying

, LIN

Jian-hua.

Pile defect diagnosis based on wavelet analysis and neural networks. Journal of Vibration and Shock, 2002, 21(3): 11-17. ]

本文利用多分辨率分析提取桩基低应变动测信号功率谱的特征,作为BP神经网络的输入.通过对模型桩桩身缺陷信息的学习,预测诊断桩身缺陷类型.此外,利用小波变换的极值点诊断桩身的缺陷位置及利用小波包分析提取桩顶速度时域曲线的时、频域特征输入神经网络,通过模型桩的学习,预测诊断桩身缺损程度.工程应用实例表明,该法有一定的精度,是一种有效的桩身质量判别方法.

2012

0.0

0.261

曲静, 王昱. 方差分析周期外推法在春季降水量预报中的应用[J]. 甘肃科学学报, 2012, 24(2): 68-71.

[QU

Jing

, WANG

. Application of variance analysis and extrapolation method to forecasts of spring precipitation. Journal of Gansu Sciences, 2012, 24(2): 68-71. ]

选取西安市1990～2009年共20年春季(3～5月)降水量资料,采用方差分析法,按不同长度周期进行排列,求出F值并进行检验,得出春季总降水量变化:以6年为主周期,8年、7年为校正周期,将所得的3个周期的稳定位相值叠加,再用外推法对西安2010年、2011年春季降水量进行预报.结果表明:应用方差分析制作的春季降水量趋势预报方法,历史拟合率为95％,其中1996年、2002年和2003年定量预报偏差较大,为20～30 mm;在2010年、2011年的试报中,定性预报效果较好,2010年定量预报偏差较大,为37.3 mm;用此方法作预报时若配合其他预报方法使用,效果会更好.该方法对实际业务预报春季降水量具有一定的参考价值.

... 选取得太高可能会得不到理想的周期个数^[9] ...

2002

0.0

... 功率谱周期方法是分析时间序列常用的方法,它通过快速傅里叶变换研究频率与自相关函数的傅氏变换之间的关系,根据功率谱图的特点直观地揭示出离散数据序列的周期性^[10],可快速、准确地识别出径流序列的周期性 ...

2007

0.0

0.656

燕爱玲, 黄强, 王义民. 河川径流演变的非趋势波动分析[J]. 水力发电学报, 2007, 26(3): 1-4.

[YAN

Ai-ling

, HUANG

Qiang

, WANG

Yi-min

. Detrended fluctuation analysis of river runoff evolvement. Journal of Hydroelectric Engineering, 2007, 26(3): 1-4. ]

运用非趋势波动分析法,对黄河上游河川径流近百年月平均流量序列进行了分析,揭示了河川径流的长程相关性及其内在规律性.研究结果表明:黄河上游近百年河川径流序列波动的标度指数a=0.5862,存在内在的正长程相关性,长程幂律关系至少可持续54月或4.5年;大于54月尺度区间的标度发生改变,可能是不同时空尺度下信号突变或序列长度受限所致,这也从某种程度上体现了河川径流系统演变过程中复杂的物理机制.

... 河川径流序列的演变和波动的另一个重要特性为长程相关性（持久性）^[11] ...

1993

2.326

0.0

... 去趋势波动分析方法（Detrended Fluctuation Analysis, DFA）^[12],随后在自然科学和社会科学等领域得到了广泛的应用,取得了重要的研究进展 ...

2002

1.722

0.0

... 与R/S分析方法相比,DFA可以将不同阶（1~p阶）的外在趋势从原有序列中剔除,从而结果更加真实、可靠,优于R/S分析法^[13] ...

2008

0.0

... 目前在泾河径流的特性分析方面,主要集中于径流的趋势或周期演变分析^{[14,15,16,17,18]}以及分形特性分析^[19]等方面,如李雯分析了泾河流域张家山站年径流量的年际变化和年内变化特征^[14] ...

2008

0.0

... 李勋贵采用Mann-Kendall方法分析了泾河流域杨家坪、雨落坪和张家山站径流序列的变化趋势^[15] ...

2010

0.0

... 吕静渭采用滑动平均法和Kendall秩次相关检验法分析了泾河流域年径流量的变化趋势,并基于小波分析研究了年径流量的变化周期^[16] ...

... 其他研究者^[16,17,18]也指出泾河流域年径流具有2或3 a的变化周期,与本文的研究结果相一致 ...

2010

0.0

0.373

吕静渭, 马孝义, 高文强, 等. 近70年来泾河年径流量周期变化的小波分析[J]. 人民黄河, 2010, 32(2): 49-50, 67.

[Lü

Jing-wei

, MA

Xiao-yi

, GAO

Wen-qiang

, et al. Wavelet analysis of periodicity changes from annual runoff over 70 years in the Jinghe watershed. Yellow River, 2010, 32(2): 49-50, 67. ]

利用Morlet复小波变化法对泾河流域1933-2000年的年径流量变化进行了多尺度分析,探讨了年径流量在不同时间尺度上波动变化的特征.结果表明:13年、32年左右的主周期变化和3年、21年左右的次周期变化共同决定着泾河年径流量的丰枯变化特征;2000年以后的几年内泾河年径流量仍处于偏枯期.

... 其他研究者^[16,17,18]也指出泾河流域年径流具有2或3 a的变化周期,与本文的研究结果相一致 ...

2013

0.0

0.373

陈晨, 罗军刚, 解建仓, 等. 泾河流域近80a径流变化趋势及特征分析[J]. 人民黄河, 2013, 35(1): 26-28, 38.

[CHEN

Chen

, LUO

Jun-gang

, XIE

Jian-cang

, et al. Chang trend and characteristics of runoff sequences over 80 years in the Jinghe River Basin. Yellow River, 2013, 35(1): 26-28, 38. ]

基于泾河流域1932-2010年近80 a的实测径流数据,采用Morlet小波对泾河流域径流进行周期、丰枯变化及突变点分析,采用Db3小波对最大尺度下的低频成分进行重构,获得泾河流域的径流变化趋势,并应用Kendall秩次相关分析法对径流进行显著性检验.结果表明:在近80 a的研究时段中,泾河流域年径流量总体呈现明显减小趋势,但在2000年开始年径流量有所增大；在泾河流域的年径流序列多尺度分析中,同一时段径流变化的趋势有所不同,2 a周期年径流丰枯变化存在比较明显的局部差异,7 a周期经历了由弱到强,之后又逐渐减弱的过程,12 a和20 a周期逐渐增强.

... 2010年的实测径流序列的周期、丰枯变化及突变点进行了分析^[18] ...

... 其他研究者^[16,17,18]也指出泾河流域年径流具有2或3 a的变化周期,与本文的研究结果相一致 ...

2011

0.0

0.418

陈刚, 胡素端, 王怡璇, 等. 基于GIS的泾河流域径流过程分形特征研究[J]. 水资源与水工程学报, 2011, 22(3): 124-127.

[CHEN

Gang

, HU

Su-duan

, WANG

Yi-xuan

, et al. Research on fractal characteristics of runoff process in the Jinghe River Basin based on GIS. Journal of Water Resources and Water Engineering, 2011, 22(3): 124-127. ]

运用分形理论对水文系统演化的非线性规律进行研究,可全面地揭示水文动力系统的复杂运动特征.论文首先运用DPS数据处理软件选取不同频率(25%、50%、75%)的典型年,整编泾河张家山站不同典型年的1日、7日、15日径流资料,再运用ARCGIS中的Hawthtool工具计算各频率典型年的1日、7日、15日径流过程分维数,以及1932年-1999年的年径流序列分维数,得出:平水年水量分配较枯水年和丰水年更不均匀,在这些年份里,积极准备防洪抗旱,实现合理的水资源调节,有着重要的现实意义.并在此基础上,进一步分析泾河流域径流过程的分形特征,得出:分维数是一段时间内自然因素和人类活动共同作用于径流过程的综合反映.研究对于指导研究区水资源的调控有着重要的意义.

... 1999年泾河张家山水文站1日、7日和15日径流的分形特征进行了研究^[19] ...

2003

0.0

庄新田, 黄小原. 证券市场的标度理论及实证研究[J]. 系统工程理论与实践, 2003, 23(3): 1-8.

[ZHUANG

Xin-tian

, HUANG

Xiao-yuan

. Scale theory and empirical research in the securities market. Systems Engineering-theory & Practice, 2003, 23(3): 1-8. ]

Scaling invariance is found in a wide range of systems from nature to society, of economy and finance, is the power law behavior of a particular observable, financial complexity is promulgated. Applying fractal theory, we approach self-similar and scale invariance of securities market and analyze three kinds of scale index i.e autocorrelation index, Hurst index, on the basis of scale index of DFA calculation method. We improve Hurst index. Based on time series standard deviation. DFA is spreaded into dynami...

运用分形理论探讨证券市场的自相似性与标度不变性 ,分析三种标度指数 ,即自相关指数、Hurst指数、基于 DFA算法的标度指数 .基于标准差时间序列改进 Hurst指数 ,将 DFA推广为动态递推算法 .利用三种标度指数对国内沪深股市进行实证研究 .结果表明 ,沪深股市收益率均不服从正态分布 ,在跨时间尺度的股价指数之间存在着相关性 ,表现为分形时间序列 ,说明其背后所隐含的政策导向影响中国股票市场的特征 .

... 值与自相关函数有着密切的关系^[20,21]：当 0α0 ...

2005

0.0

何越磊, 姚令侃, 苏凤环. 强沙尘暴时序的标度不变性分析[J]. 系统工程理论与实践, 2005, 25(7): 125-130.

[HE

Yue-lei

, YAO

Ling-kan

, SU

Feng-huan

. Scale invariance analysis of the time series of severe sand and dust storm. Systems Engineering-theory & Practice, 2005, 25(7): 125-130. ]

The time series of severe sand and dust storm has complicated undulatory property. We analyze the time series of severe sand and dust storm occurred in the north of China in 49 years by the means of multifractal detrended f1uctuation analysis (MF-DFA). It is found that the time series is long range correlation. We affirm the severe sand and dust storm is multifractal. The strange multifractal spectrum is educed. The strong breeze, sand origin and thermodynamic instability are the principal factors forming s...

强沙尘暴规模的时间序列具有复杂的波动性.运用多重分形消除趋势波动分析法分析我国北方近49年来的强沙尘暴序列.发现序列具有长程相关性;并确认强沙尘暴是多重分形过程,进而得出序列的多重分形谱.在此基础上,探讨了序列长程相关性和多重分形特征与强风、沙源和热力不稳定等我国北方强沙尘暴形成的主要因素之间的联系.

... 值与自相关函数有着密切的关系^[20,21]：当 0α0 ...

2015

0.0

0.372

李勋贵, 魏霞. 基于系统周界观控模型的径流还原方法[J]. 水利水电技术, 2015, 46(1): 11-16.

[LI

Xun-gui

, WEI

Xia

. Runoff restoration method based on observability-controllablity model of periphery. Water Resources and Hydropower Engineering, 2015, 46(1): 11-16. ]

... 尽管该法存在调查的年份较长、调查的数据和涉及的参数繁多、在还原时可能会引起累积误差等不足,但其在人类活动影响较小的情况下有较高的还原精度,在人类活动影响较大的区域,还原成果的总体趋势不变^[22] ...

2009

0.0

1.672

张明, 张建云, 金菊良. 基于遗传熵谱估计的年径流周期识别[J]. 水科学进展, 2009, 20(3): 337-342.

[ZHANG

Ming

, ZHANG

Jian-yun

, JIN

Ju-liang.

Genetic entropy spectral estimation method and its application to annual runoff periodic identification. Advances in Water Science, 2009, 20(3): 337-342. ]

An improved entropy spectral estimation method,Genetic Entropy Spectral estimation(GES),is proposed to identify the implicit periods in annual runof time series.The method is based on the accelerating genetic algorithm(AGA),which is mainly used to optimize the parameters of maximum entropy spectral analysis method(MESA),and minimize the four equivalent conditions of MESA.Compared to the traditional variation spectral method and Burg spectral method,the entropy estimation results based on the improved method is not depend on the selection of initial value,further more,the method has high adaptability for data length,signal noise ratio and initial phases.Taking Houdacheng station in the Sanchuanhe River basin as a case,an annual runof series from 1956 to 2000 is studied with the method.And results show that there are two prominent periods of 12.29 years and 2.67 years in the time series with 95% confidence level.GES method can provide a new approach for variation law and phases analysis study of runof series.

为识别年径流量序列的隐含周期,提出基于加速遗传算法的熵谱估计算法,与传统的方差谱和Burg谱相比,该方法由熵谱分析的4个等价条件构建多目标函数,并以加速遗传算法作为优化算法,谱估计结果不依赖于初始值的选取,对数据长度、信噪比和初相位有较强的适应性。在三川河流域后大成站1956-2000年径流量序列周期识别中的应用结果表明,在95%的置信检验水平下,序列中存在着12.29年和2.67年的显著隐含周期,为三川河流域年径流的变化规律和变化的阶段性研究提供了一条新的定量研究手段。

... 泾河流域位于黄河中游地区,受到来自西太平洋副热带高压、青藏高原高度场以及印度槽的综合影响^[23],流域降水量和径流量序列中存在的2 ...

2010

0.0

1.791

杨明金, 张勃. 黑河莺落峡站径流变化的影响因素分析[J]. 地理科学进展, 2010, 29(2): 166-172.

[YANG

Ming-jin

, ZHANG

Bo.

The study on affecting factors of runoff changes at Yingluoxia Station of Heihe River. Progress in Geography, 2010, 29(2): 166-172. ]

Based on the runoff data covering 45 years at Yingluoxia Station at the main stream of the Heihe River, this paper studied the global change, sunspot activity, ENSO cycle and underlying surface variation affecting the change of mountainous runoff at the main stream of the Heihe River using correlation analysis, cross-spectrum analysis, statistical law analysis and precipitation-runoff double mass analysis. The results showed that: (1) The global change had significant influence on the runoff of Yingluoxia Station; (2) The runoff of Yingluoxia Station and the number of sunspots were closely related with the vibration periods of 2 and 3.3 years, but vibration period change of the number of sunspots lagged behind the runoff of Yingluoxia Station; (3) The ENSO cycle had some influence on the runoff of Yingluoxia Station, while the influence of El Nino and La Nina sustained shortly, which could only exert some effect on the runoff of Yingluoxia Station when they occurred obviously, but they affected the next year's runoff weakly; (4) The underlying surface variation had a weak influence on the runoff of Yingluoxia Station.

以黑河干流出山口径流控制站莺落峡水文站1960-2004年45年的径流序列为基础数据，采用相关分析、交叉谱分析、统计规律分析、降水—径流双累积曲线法等研究了全球变化、太阳黑子活动、ENSO循环和下垫面变化对黑河干流出山径流变化的影响。结果表明：①全球变化对莺落峡站径流变化影响较大；②莺落峡站年径流与太阳黑子相对数两序列在2年和3.3年两个振动周期上存在显著的相关关系，但在这两个存在显著相关关系的振动周期上太阳黑子相对数的周期波动变化都落后于莺落峡站年径流的周期波动变化；③ENSO循环对莺落峡站年径流变化有一定的影响，但是，El Nino事件和La Nina事件对莺落峡站年径流的影响时间持续较短，对事件发生当年的径流变化影响较大，对事件发生次年的径流变化影响较小；④流域下垫面变化对莺落峡站年径流量的变化影响较小。

... 2 a周期可能与气候系统中的海-气相互作用的准2 a振荡周期^[24,25]以及厄尔尼诺事件的2~4 a变化周期^[26]有关 ...

2003

1.459

1.057

... 2 a周期可能与气候系统中的海-气相互作用的准2 a振荡周期^[24,25]以及厄尔尼诺事件的2~4 a变化周期^[26]有关 ...

2008

0.0

... 2 a周期可能与气候系统中的海-气相互作用的准2 a振荡周期^[24,25]以及厄尔尼诺事件的2~4 a变化周期^[26]有关 ...

... 7 a周期的变化可能与厄尔尼诺事件的2~4 a变化周期^[26]以及副高脊线位置的3 a准周期^{[27,28,29,30]}有关 ...

1982

0.0

1.979

徐国昌, 董安祥. 我国西部降水量的准三年周期[J]. 高原气象, 1982, 1(2): 11-16.

[XU

Guo-chang

, DONG

An-xiang.

The quasi-three year period of precipitation in the west of China. Plateau Meteorology, 1982, 1(2): 11-16. ]

本文利用我国西部110°E以西70个站的资料,用周期图和功率谱方法计算分析了降水量周期,发现最显著的周期是准三年周期,主要表现在35°N以北,即青藏高原的北侧,高原东北侧最明显。准三年周期主要表现在春季和夏季。从三十年代到七十年代准三年周期比较稳定。它的形成可能与南亚高压脊线准三年周期的南北振荡有关。另外,我国西部还存在着一个次要的周期是10—13年周期。

... 7 a周期的变化可能与厄尔尼诺事件的2~4 a变化周期^[26]以及副高脊线位置的3 a准周期^{[27,28,29,30]}有关 ...

1994

0.0

1.073

梁建茵. 6月西太平洋副高脊线的年际变化及其对华南降水的影响[J]. 热带气象学报, 1994, 10(3): 274-279.

[LIANG

Jian-yin

. The interannual variations of the subtropic high ridge position over western pacific in June and its influence on precipitation in south of China. Journal of Tropical Meteorology, 1994, 10(3): 274-279. ]

In this paper the interannual variations of subtropic high ridge position over western Pacific in June are investigated by using the data of the ridge based on 500 hPa height from 1951 to 1991. The results indicate that 41-year averaged ridge position is located in 20°N, the oscillations of the ridge position exhibit 32-year, 5.3-year, 2-3year period and its variations are associated with 500 hPa height, SST of South China Sea and western Pacific. As the ridge locates more to the north (>20°N), there will be less precipitation in south of China, and as the ridge is more to south (<20°N), there will be much more precipitation.

用1951-1991年6月份500hPa位势高度资料取得了西太平洋副热带高压脊线位置资料序列,分析了脊线位置的变化。分析结果发现副高脊线位置与500hPa位势高度场、海面温度等关系密切。脊线位置具有显着的32年、5.3年、3.2年和2.3年振荡周期。6月份副高脊线偏北(南)华南降水偏少(多).

... 7 a周期的变化可能与厄尔尼诺事件的2~4 a变化周期^[26]以及副高脊线位置的3 a准周期^{[27,28,29,30]}有关 ...

1995

0.0

1.073

赵振国, 陈国珍. 初夏西太平洋副高南北位置长期变化的成因及预报[J]. 热带气象学报, 1995, 11(3): 223-230.

[ZHAO

Zhen-guo

, CHEN

Guo-zhen

. The cause and forecast of long-term change of the latitudinal position of west Pacific subtropical high in early summer. Journal of Tropical Meteorology, 1995, 11(3): 223-230. ]

In this paper, using data of monthly mean geopotential height and SST in a statistic-relation analysis, the regularity and cause of long-term change of the latitudinal position of West Pacific subtropical high in early summer have been studied. The results indicate that there seems to have about 11-year and 3-5 year quasi-lleriods. The quasi-periodicity is closely associated with the changes in solar activity, SST in the eastern equatorial Pacific and the geopotential height in the upper troposphere in central and eastern tropical Pacific in Northern Hemisphere. The high's position tends to be more to the south of its normal location corresponding to peak years of sunspot and warm episodes of SST and positive phases of the geopotential height. Vice verse. According to the above conclusion, the forecast criterion of the ridge line of West Pacific Subtropical High for June has been found. Its foreeast results are satisfactory.

利用月平均高度场和海温场资料,通过统计相关分析,探讨了初夏西太平洋副热带高压南北位置长期变化的规律及其成因,结果表明,初夏副高南北位置存在着11年左右和3-5年的准周期振荡,这种周期变化分别与太阳活动、海洋下垫面和对流层上部位势高度场类似的周期振荡相吻合。太阳黑子高值年、赤道东太平洋暖水期、热带中东太平洋对流层上部位势高度偏高阶段,初夏西太平洋副高位置偏南,反之偏北。最后建立了6月份副高脊线的预报方法。

... 7 a周期的变化可能与厄尔尼诺事件的2~4 a变化周期^[26]以及副高脊线位置的3 a准周期^{[27,28,29,30]}有关 ...

2005

0.0

0.612

许金镜, 林新彬, 温珍治. 夏季副高位置的变化规律及其与福建干旱的关系分析[J]. 台湾海峡, 2005, 24(3): 363-369.

[XU

Jin-jing

, LIN

Xin-bin

, WEN

Zhen-zhi.

Variation of subtropical high and an analysis of its relationship with drought in Fujian during summer. Journal of Oceanography in Taiwan Strait, 2005, 24(3): 363-369. ]

本文应用子波分析和功率谱等方法揭示夏季副高脊线位置的变化规律,进而分析脊线位置与福建夏季干旱的关系.主要结论有:(1)夏季副高脊线位置在20世纪80年代是异常偏南的频发时段,20世纪60年代和90年代是异常偏北的频发时段;且存在较为明显的准3～5、7、9a和13a周期振动,特别是准9a的周期振动相当显著(2)夏季副高脊线位置处于偏南(北)状态时,福建夏季易于(不易于)出现干旱;(3)夏季副高南界位置处于偏南(北)状态时,将影响到福建夏季降水;2003年夏季副高南界位置偏南与福建夏季严重干旱有着密切的联系,其振动对中低纬度地区值得注意.

... 7 a周期的变化可能与厄尔尼诺事件的2~4 a变化周期^[26]以及副高脊线位置的3 a准周期^{[27,28,29,30]}有关 ...

2012

0.0

... 值与周安康^[31]采用1960#cod#x02014 ...

... 同时,周安康^[31]还获得渭河干流的咸阳站、华县站和北洛河的状头站的标度指数#cod#x003b1 ...

2011

0.0

李鹏, 赵雪花. 兰村站天然径流演变长程相关性分析[J]. 科技情报开发与经济, 2011, 21(30): 179-181.

[LI

Peng

, ZHAO

Xue-hua.

Long-range correlation analysis on Lancun Station’s natural runoff evolution. Sci-Tech Information Development & Economy, 2011, 21(30): 179-181. ]

采用非趋势波动分析法(DFA)对汾河上游兰村站45年的天然月径流量进行了长程相关性分析,并计算出了标度指数.结果表明汾河上游径流演变具有正长程相关性,汾河上游历史径流量的演变呈衰减趋势状态基本保持一致,并会在未来的演变中继续保持这种衰减趋势状态的变化规律.

... 同时,李鹏和赵雪花^[32]得到1956#cod#x02014 ...

2007

0.0

1.841

佟春生, 黄强, 刘涵, 等. 黄河径流序列标度不变性分析及趋势预测研究[J]. 自然资源学报, 2007, 22(4): 634-639.

[TONG

Chun-sheng

, HUANG

Qiang

, LIU

Han

, et al. Scale invariant analysis and runoff trend prediction of the runoff time series in the Yellow River. Journal of Natural Resources, 2007, 22(4): 634-639. ]

长期以来,影响黄河干流梯级电站可持续发展的因素,除了关键技术因素、经济因素和环境因素,还有对未来径流趋势的认知不足.可见研究黄河干流径流变化趋势,对于黄河干流梯级电站可持续发展具有重要的现实意义.论文利用非趋势的波动分析法,对黄河干流贵德、头道拐和花园口3个水文站径流的标度不变性和未来变化趋势进行了分析和预测.结果显示,3个水文站的径流量将会减少,这将对黄河干流梯级电站可持续发展不利.

... 553 2,佟春生等^[33]采用DFA方法获得1920#cod#x02014 ...

2005

0.0

... 有研究表明,泾河流域径流波动的这种持久性（长程相关性）,与径流系统的复杂性有一定联系^[34] ...

2012

0.0

... 7 a周期可能是外力作用下（如厄尔尼诺、南方涛动等^[35,36,37]）使2 ...

1993

0.0

2.498

李月洪, 张正秋. 百年来中国黄河流域区域性旱涝气候突变[J]. 地理科学, 1993, 13(4): 315-321.

[LI

Yue-hong

, ZHANG

Zheng-qiu

, Abrupt climatic change of drought and flood in the Huanghe River Basin during the last 10years. Scientia Geographica Sinica, 1993, 13(4): 315-321]

In this paper,the drought/flood indexes for the divisions in the Huanghe River Basin during the last 100 years (1891-1990) are analysed to reveal abrupt climatic change using the Mann-Kendall Test.It is found that there existed abrupt climatic change of drought/flood in 1910 and 1912 over the middle and lower reaches respectively,but no such obvious abrupt climatic change is found over the upper reaches.These facts show that there existed abrupt climatic changes of drought/flood for most parts of the basin during the 1910s,which were jumps from flood to drought phases.Meanwhile, it is should be pointed out that the jump was not non-local event in the basin.In addition,the possible reasons causing the jumps are discussed.By analysing the South Oscillation Index and the air temperature of the Northern Hemisphere using the same test, one can see that their abrupt changes occurred earlier than that of the drought/flood,indicating that these may be improtant background conditions for the event of abrupt climatic change of drought/flood.

通过对近百年来黄河流域各区域旱涝气候突变特征的研究,表明该流域的大部分地区旱涝气候变化在本世纪10年代内出现突变现象,而且是从一个相对的偏涝期进入偏早期的转变。并且初步分析了黄河流域出现旱涝气候突变的可能成因。

... 7 a周期可能是外力作用下（如厄尔尼诺、南方涛动等^[35,36,37]）使2 ...

2002

0.0

2.412

蓝永超, 马全杰, 康尔泗, 等. ENSO循环与黄河上游径流的丰枯[J]. 中国沙漠, 2002, 22(3): 262-266. ]

[LAN

Yong-chao

, MA

Quan-jie

, KANG

Er-si

, et al, Relationship between ENSO cycle and abundant or low runoff in the upper Yellow River. Journal of Desert Research, 2002, 22(3): 262-266]

分析了黄河上游径流主要形成区-_唐乃亥以上流域的气象和水文特性,在此基础上,根据El Nino现象及 La Nina现象与黄河上游径流的丰枯的对应关系,探讨了ENSO事件对黄河上游径流的影响.统计结果表明,ENSO现象与黄河上游唐乃亥以上流域的径流丰枯有着密切的关系.总体而言,伴随着El Nino事件的发生,黄河上游出现枯水的概率较大,而黄河上游的洪水常伴随着La Nina 事件发生.

... 7 a周期可能是外力作用下（如厄尔尼诺、南方涛动等^[35,36,37]）使2 ...